[손으로 푸는 확률분포] 정규분포 (2) 과녁을 이용한 유도

정규분포를 유도하는 방법은 두 가지가 있습니다. 과녁 맞추기를 이용한 유도와 이항분포를 이용한 유도입니다. 두 유도방법 모두 '정규분포가 무엇인가' 라는 질문에 좋은 답변을 제공해줍니다. 오늘은 첫번째 방법인 '과녁 맞추기를 이용한 유도'를 알아봅시다. 

 

우리가 어떤 물체의 길이를 측정하는 상황이라고 해봅시다. 우리가 측정할 때 마다 측정값은 조금씩 달라질 것입니다. 측정에는 항상 오차가 있기 때문입니다. 측정을 무한히 반복했다고 가정하고, 측정된 값들을 확률분포로 만들고 싶었습니다. 실제로 측정을 무한 번 하지는 않을 거구요. 그럴듯한 수학 모델을 만들어 볼 겁니다.

 

그럴듯한 수학 모델을 만들기 위해 물체의 길이를 측정하는 것과 비슷한 상황 하나를 생각해냈습니다. 바로 '과녁 맞추기' 입니다. 아래와 같은 과녁이 있다고 합시다. 

 

 

우리는 이 과녁의 중심을 맞추고 싶은 상황입니다. 우리가 화살쏘기에 숙련된 전문가라고 가정합시다. 중앙을 겨냥해서 화살을 쏠 것입니다. 그러나 아무리 전문가라고 해도 항상 과녁 중앙에 화살을 맞출 수는 없습니다. 아래 그림 처럼 화살이 빗나가는 경우도 있을 것입니다. 

 

 

이러한 상황을 확률분포로 만들어봅시다. 위 상황을 확률분포로 만들기 위해 아래와 같은 두가지 가정을 하겠습니다. 

 

1) 과녁의 중심에서 멀어질 수록 맞출 확률이 낮다. 

2) 과녁의 중심에서 거리가 같은 두 점이 있다면, 이 두 점의 확률은 동일하다. 

 

딱 이 두가지 조건만을 이용해서 확률분포를 유도해 보았습니다. 어떤 분포가 하나 유도 됐는데요. 그 분포가 바로 정규분포입니다. 정규분포가 무엇인지 감이 오시나요? 과녁의 중심은 참값, 과녁에서 벗어나는 값이 생기는 이유를 오차라고 할 수 있습니다. 따라서 정규분포는 참값과 오차의 분포라고 할 수 있습니다. 우리가 원하는 어떤 참값이 있는데, 오차 때문에 참값에서 떨어지 값들도 발생하게 되는 겁니다. 참값에서 멀어질 수록 발생 확률은 낮습니다. 이런 상황을 수학적으로 표현해보았더니 오늘날 우리가 잘 아는 정규분포가 된 것입니다. 

 

정규분포가 무엇인지는 이미 이해했습니다. 수학적인 유도는 재미삼아 해봅시다. 

 

과녁 위 어느 한 점 $f(x,y)$에 화살이 맞을 확률밀도를 $f(x,y)$라고 놓겠습니다. 확률밀도함수를 전체 구간(도메인)에 대해 적분한 값은 1이므로 아래 등식이 성립합니다. 

 

$\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }f(x,y)dxdy=1$

 

우리는 지금부터 $f(x,y)$를 유도할 것이구요. 증명은 아래 순서로 진행됩니다. 

 

1. x의 주변확률분포

2. y의 주변확률분포

3. 독립성가정

4. 거리가 r인 곳의 확률밀도함수

5. 계수 A 구하기

6. 계수 C 구하기

7. $f(x)$ 구하기

 

1. x의 주변확률분포

확률밀도함수 $f(x,y)$를 y의 전체구간에 대해 적분해봅시다. 

 

$\int_{-\infty }^{\infty }f(x,y)dy$

 

y에 대해 정적분을 한 것이므로, 결과는 x만의 함수가 됩니다. 계산 결과를 $f_{x}(x)$ 라고 놓겠습니다.

 

$\int_{-\infty }^{\infty }f(x,y)dy=f_{x}(x)$

 

$f_{x}(x)$를 x의 주변확률분포라고 합니다. 이 함수의 의미를 생각해봅시다. x에 어떤 값 a를 대입해봅시다. $f_{x}(a)$인데요. $f_{x}(a)$는 아래 그림과 같이 $x=a$ 인 선 위에 화살이 맞을 확률밀도를 의미합니다. 

 

 

2. y의 주변확률분포

확률밀도함수 $f(x,y)$를 x의 전체구간에 대해 적분해봅시다. 

 

$\int_{-\infty }^{\infty }f(x,y)dx$

 

x에 대해 정적분을 한 것이므로, 결과는 y만의 함수가 됩니다. 계산 결과를 $f_{y}(y)$ 라고 놓겠습니다.

 

$\int_{-\infty }^{\infty }f(x,y)dx=f_{y}(y)$

 

$f_{y}(y)$를 y의 주변확률분포라고 합니다. 이 함수의 의미를 생각해봅시다. y에 어떤 값 a를 대입해봅시다. $f_{y}(a)$인데요. $f_{y}(a)$는 $y=a$ 인 선 위에 화살이 맞을 확률밀도를 의미합니다. 

 

원점으로 부터의 거리에 따라 확률이 변한다고 가정했기 때문에, x방향으로 멀어지는 것과 y방향으로 멀어지는 것의 영향이 동일합니다. 따라서 $f_{x}(x)$ 와 $f_{y}(y)$ 는 동일한 함수입니다. 앞으로는 아래첨자를 생략하고 $f(x),f(y)$ 라고 놓겠습니다. 

 

$f_{x}(x)=f(x)$

$f_{y}(y)=f(y)$

 

3. 독립성 가정

한가지 가정을 추가합시다. 확률변수 x와 y가 서로 독립이라는 가정입니다. 독립성 가정에 의해 아래 등식이 성립합니다. (참고: hsm-edu.tistory.com/1178?category=770915)

 

$f(x,y)=f(x\cap y)=f(x)f(y)$

 

사실은 위 수식을 얻기 위해 1,2,3번 과정을 거친 것입니다. 

 

4. 거리가 r인 곳의 확률밀도 함수

함수를 하나 더 정의하겠습니다. 과녁의 중심에서 부터 거리가 $r$인 곳의 확률밀도를 $g(r)$ 이라고 놓겠습니다. 원점에서 부터의 거리가 $r$인 어떤 좌표를 $(x,y)$라고 놓는다면 아래 등식이 성립합니다.

 

$g(r)=f(x,y)$

 

 

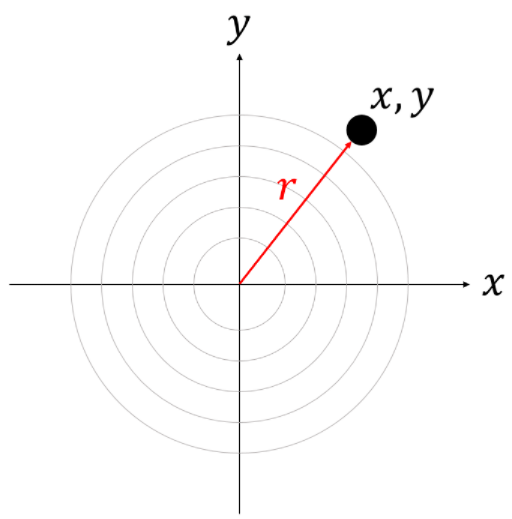
확률변수 x,y가 서로 독립이므로 아래 등식이 성립합니다. 

 

$g(r)=f(x)f(y)$

 

이때 x축과 r방향 사이의 각도를 $\theta$ 라고 놓는다면 x와 y를 아래와 같이 나타낼 수 있습니다. 

 

$x=r \cos(\theta)$

$y=r \sin(\theta)$

 

$g(r)=f(x)f(y)$ 식의 양변을 $\theta$로 미분하겠습니다. $g(r)$은 $\theta$와 무관한 함수이므로 미분하면 0이 됩니다. 

 

$0=\frac{df(x)}{d\theta}f(y)+f(x)\frac{df(y)}{d\theta}$

 

체인룰을 적용합시다.

 

$0=\frac{df(x)}{dx}\frac{dx}{d\theta} f(y)+f(x)\frac{df(y)}{dy}\frac{dy}{d\theta}$

 

아래와 같이 변형합시다.

 

$0=f'(x)\frac{dx}{d\theta} f(y)+f(x)f'(y)\frac{dy}{d\theta}$

 

아래와 같이 $\theta$로 미분된 항에 있는 $x$와 $y$를 $r$과 $\theta$에 대한 식으로 바꿔줍니다. 

 

$0=f'(x)\frac{dr \cos(\theta)}{d\theta} f(y)+f(x)f'(y)\frac{dr \sin(\theta)}{d\theta}$

 

$\theta$로 미분합시다.

 

$0=f'(x)(-r \sin\theta) f(y)+f(x)f'(y)(r \cos\theta)$

 

아래와 같이 양변을 정리합시다.

 

$\frac{f'(x)}{f(x)}\frac{r \sin\theta}{r \cos\theta}=\frac{f'(y)}{f(y)}$

 

r을 약분합시다. 

 

$\frac{f'(x)}{f(x)}\frac{\sin\theta}{\cos\theta}=\frac{f'(y)}{f(y)}$

 

$\frac{\sin\theta}{\cos\theta}$는 $\tan\theta$이므로 아래와 같이 변형합시다. 

 

$\frac{f'(x)}{f(x)} \tan\theta=\frac{f'(y)}{f(y)}$

 

$\tan\theta$ 는 $\frac{y}{x}$이므로 아래와 같이 변형할 수 있습니다. 

 

$\frac{f'(x)}{f(x)}\frac{y}{x}=\frac{f'(y)}{f(y)}$

 

$y$로 양변을 나눠줍시다. 

 

$\frac{f'(x)}{f(x)}\frac{1}{x}=\frac{f'(y)}{f(y)}\frac{1}{y}$

 

x와 y에는 모든 실수가 올 수 있기 때문에, 어떤 값을 넣어도 위 등식이 성립한다는 의미입니다. 만약 좌변이 x에 대한 변수이고, 우변이 y에 대한 변수라면 등식이 성립하지 않는 경우가 존재하게 됩니다. 따라서 좌변과 우변은 상수입니다.

 

$\frac{f'(x)}{f(x)}\frac{1}{x}=\frac{f'(y)}{f(y)}\frac{1}{y}=C$

 

x에 대해서만 생각해봅시다. 아래 등식입니다. 

 

$\frac{f'(x)}{f(x)}\frac{1}{x}=C$

 

양변에 x를 곱해줍시다.

 

$\frac{f'(x)}{f(x)}=Cx$

 

양변을 x에 대해 적분합시다.

 

$\mathrm{ln}f(x)=\frac{1}{2}Cx^{2}+D$

 

f(x)에 대해 정리하면 아래와 같습니다. 

 

$f(x)=e^{\frac{C}{2}x^{2}}e^{D}$

 

$e^{D}$는 상수이므로, 상수 A로 간단히 표현하겠습니다. 

 

$f(x)=Ae^{\frac{C}{2}x^{2}}$

 

벌써 모양이 정규분포스러워 졌습니다. 

 

5. 계수 A 구하기

먼저 A의 부호를 판별해봅시다. $f(x)$는 확률밀도함수이기 때문에 음수값을 가질 수 없습니다. 따라서 항상 양수여야 합니다. $e^{\frac{C}{2}x^2}$ 는 항상 양수이므로, A도 항상 양수입니다. 

$A>0$

 

C의 부호도 판별해봅시다. $f(x)=Ae^{\frac{C}{2}x^2}$에서 만약 C가 양수라면 x가 커질 수록 $f(x)$는 한없이 커집니다. x가 커질 수록 전체 값은 작아지는 것이 초기에 설정한 조건이었습니다. x가 커질 수록 전체 값이 작아지려면 C는 음수여야 합니다.

 

$C<0$

유도를 편하게 하기 위해 -c를 k 로 치환하여 양수 k를 사용하겠습니다. 치환한 함수는 아래와 같습니다. 

$f(x)=Ae^{-\frac{k}{2}x^2}$

 

$f(x)$는 확률밀도함수이므로, 전체 x값에 대해 적분하면 1이 됩니다. 수식으로 나타내면 아래와 같습니다. 

$\int_{-\infty}^{\infty}f(x)dx=1$

우리는 아래 두가지 가정을 했습니다. 

1) 과녁의 중심에서 멀어질 수록 맞출 확률이 낮다. 
2) 과녁의 중심에서 거리가 같은 두 점이 있다면, 이 두 점의 확률은 동일하다. 

두번째 가정에 의해 중심에서 거리가 같으면 확률이 동일합니다. 따라서 $f(x)$ 는 대칭함수입니다. 대칭함수에서는 적분구간을 0부터 무한대로 바꾸고 적분값을 1/2 로 놓을 수 있습니다. 

$\int_{0}^{\infty}f(x)dx=\frac{1}{2}$

$f(x)$ 자리에 우리가 유도한 수식을 대입합시다. 

$\int_{0}^{\infty}Ae^{-\frac{k}{2}x^2}dx=\frac{1}{2}$

양변을 A로 나눠줍니다. 아래 식을 1번식이라고 놓겠습니다. 

$\int_{0}^{\infty}e^{-\frac{k}{2}x^2}dx=\frac{1}{2A}$      (1번식)

위 식의 좌변은 쉽게 적분 되지 않습니다. 적분 테크닉을 하나 사용하겠습니다. 가우스적분이라고 불리는 방법입니다. x대신 다른 문자 y를 대입하겠습니다. y도 실수 전체 구간을 갖는다고 가정하면 아래 등식이 성립합니다.  

$\int_{0}^{\infty}e^{-\frac{k}{2}y^2}dy=\frac{1}{2A} $

두 식을 곱해줍니다. 

$\left( \int_{0}^{\infty}e^{-\frac{k}{2}x^2}dx \right)\left( \int_{0}^{\infty}e^{-\frac{k}{2}y^2}dy \right)=\frac{1}{2A}\times \frac{1}{2A}=\frac{1}{4A^2}$

x와 y가 서로 독립이므로 좌변을 하나의 적분식으로 합쳐줄 수 있습니다. 

$\int_{0}^{\infty}\int_{0}^{\infty}e^{-\frac{k}{2}\left( x^2+y^2 \right)}dxdy=\frac{1}{4A^2}$

극좌표계로 바꿔줍니다. 

$\int_{0}^{\frac{\pi}{2}}\int_{0}^{\infty}e^{-\frac{k}{2}r^2}rdrd\theta=\frac{1}{4A^2}$

r에 대한 적분을 먼저 계산하면 아래와 같습니다. 

$\int_{0}^{\infty}e^{-\frac{k}{2}r^2}rdr=\left[ -\frac{1}{k}e^{-\frac{k}{2}r^2} \right]_{0}^{\infty}=\frac{1}{k}$

적분하던 원래 식에 대입합니다. 

$\int_{0}^{\frac{\pi}{2}}\frac{1}{k}d\theta=\frac{1}{4A^2}$

k는 적분변수와 무관하므로 밖으로 꺼내줍니다. 

$\frac{1}{k}\int_{0}^{\frac{\pi}{2}}1d\theta=\frac{1}{4A^2}$

적분합니다. 

$\frac{1}{k}\frac{\pi}{2}=\frac{1}{4A^2}$

$A^2$에 대해 정리합시다. 

$A^2=\frac{k}{2\pi}$

A를 구하면 아래와 같습니다. 

$A=\pm\sqrt{\frac{k}{2\pi}}$

A는 양수이므로 플러스만 해당됩니다. 

$A=\sqrt{\frac{k}{2\pi}}$    (2번식)

지금까지 구한 $f(x)$는 아래와 같습니다. 

$f(x)=\sqrt{\frac{k}{2\pi}}e^{-\frac{k}{2}x^2}$   (3번식)

 

6. 계수 C 구하기

확률변수 x의 분산은 아래와 같이 계산됩니다. 

$V[X]=\int_{-\infty}^{\infty}(x-\mu)^2f(x)dx$

확률변수 X의 확률분포 $f(x)$ 는 x축에 대해 대칭이므로 평균은 0입니다.

$V[X]=\int_{-\infty}^{\infty}x^2f(x)dx$

X의 표준편차를 $\sigma^2$으로 놓으면 아래와 같이 변형할 수 있습니다. 

$\sigma^2=\int_{-\infty}^{\infty}x^2f(x)dx$

f(x)는 x축에 대해 대칭이므로 적분구간을 0부터로 놓고 아래와 같이 변형합니다. 

$\sigma^2=2\int_{0}^{\infty}x^2f(x)dx$

양변을 2로 나눕니다. 

$\frac{\sigma^2}{2}=\int_{0}^{\infty}x^2f(x)dx$

3번 식의 $f(x)$를 대입합니다. 

$\frac{\sigma^2}{2}=\int_{0}^{\infty}x^2 \sqrt{\frac{k}{2\pi}}e^{-\frac{k}{2}x^2}dx$

적분변수와 무관한 항을 앞으로 꺼내줍니다. 

$\frac{\sigma^2}{2}=\sqrt{\frac{k}{2\pi}}\int_{0}^{\infty}x^2 e^{-\frac{k}{2}x^2}dx$

부분적분법을 이용하여 적분합니다. 

$\frac{\sigma^2}{2}=\sqrt{\frac{k}{2\pi}}\left\{\left[-x\frac{1}{k}e^{-\frac{k}{2}x^2}  \right]_{0}^{\infty}- \int_{0}^{\infty}-\frac{1}{k} e^{-\frac{k}{2}x^2}dx \right\}$

우변 괄호 안의 첫 항은 0입니다. 

$\frac{\sigma^2}{2}=\sqrt{\frac{k}{2\pi}}\left\{\int_{0}^{\infty}\frac{1}{k} e^{-\frac{k}{2}x^2}dx \right\}$

적분 안의 $\frac{1}{k}$를 밖으로 꺼내줍니다. 

$\frac{\sigma^2}{2}=\frac{1}{k}\sqrt{\frac{k}{2\pi}}\left\{\int_{0}^{\infty} e^{-\frac{k}{2}x^2}dx \right\}$

우변의 적분항은 A를 계산할 때 한번 다뤘던 식입니다. 1번식을 이용하면 아래와 같이 변형됩니다.  

$\frac{\sigma^2}{2}=\frac{1}{k}\sqrt{\frac{k}{2\pi}}\frac{1}{2A}$

2번식을 이용하여 한번 더 변형합시다. 

$\frac{\sigma^2}{2}=\frac{1}{k}A\frac{1}{2A}$

A가 약분됩니다. 

$\frac{\sigma^2}{2}=\frac{1}{k}\frac{1}{2}$

k에 대해 정리합시다. 

$k=\frac{1}{\sigma^2}$   (4번식)

 

7. $f(x)$ 구하기

3번식의 f(x) 를 가져옵시다. 

$f(x)=\sqrt{\frac{k}{2\pi}}e^{-\frac{k}{2}x^2}$

k 대신 우리가 구한 4번 식을 넣어줍니다. 

$f(x)=\sqrt{\frac{1}{2\pi \sigma^2}}e^{-\frac{1}{2\sigma^2}x^2}$

아래와 같이 변형합니다. 

$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\sigma^2}x^2}$

확률변수 X의 평균이 0이고 분산이 $\sigma^2$인 경우에 유도된 확률밀도함수입니다. 평균이 $\mu$ 라면 아래와 같이 변형됩니다. 

$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\left( x-\mu \right)^2}{2\sigma^2}}$

위 식이 평균이 $\mu$이고 표준편차가 $\sigma$인 정규분포입니다.

 

 

#강의 영상