(5) 평균
지수분포의 평균을 구해봅시다. 지수분포의 평균은 아래와 같이 구할 수 있습니다. 적분변수가 시간이므로 0부터 무한대 사이의 값을 갖습니다.

지수분포 함수를 대입하면 아래와 같습니다.

부분적분을 적용합니다.

마지막 항도 적분해줍시다.

적분상수가 무한대인 경우는 아래와 같이 극한형태로 표현할 수 있습니다.

파란 부분의 극한은 0으로 수렴한다는 것을 쉽게 알 수 있습니다. 따라서 아래와 같이 정리할 수 있습니다.

빨간 부분의 극한이 문제인데요. 아래와 같이 분수형태로 나타내봅시다.

형태를 간단하게 하기 위해 람다를 분자에 곱하고 나눠줍니다.

빨간 limit 안의 부분은 아래와 같은 극한문제와 같습니다. 이제 아래 극한을 구하면 됩니다.

직관적으로는 0이라는 것을 알 수 있습니다. exponential 이 더 빨리 증가하기 때문입니다. 그래도 0이라는 것을 수학적으로 보여봅시다. 두가지 방법이 있습니다.
1) 로피탈정리
로피탈정리를 적용합시다. 로피탈정리의 성립조건은 생략하겠습니다. 분자와 분모를 미분합시다.

2) 비교판정법
또 다른 방법은 테일러급수를 이용한 비교판정법입니다. 를 테일러전개하면 아래와 같습니다.

따라서 아래 부등식이 성립합니다.

아래와 같이 변형할 수 있습니다.

양변에 극한을 취합시다.

x가 양수라고 가정하면 아래 조건을 추가할 수 있습니다.
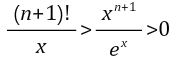
각 변에 극한을 취합시다.
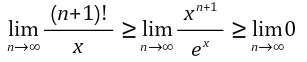
양쪽 극한값이 0으로 수렴하므로, 가운데 극한값도 0으로 수렴하게 됩니다.
지수분포의 평균을 유도하던 식으로 돌아가봅시다.
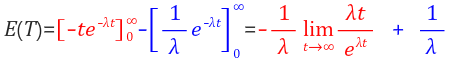
빨간 부분은 0이 됩니다. 따라서 지수분포의 평균은 아래와 같습니다.
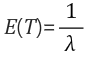
'@ 필수과목 > 손으로 푸는 확률분포' 카테고리의 다른 글
| [손으로 푸는 확률분포] 정규분포 (1) 풀리지 않았던 의문 (0) | 2021.09.25 |
|---|---|
| [손으로 푸는 확률분포] 지수분포 (8) 비기억성 (무기억성) (0) | 2021.09.25 |
| [손으로 푸는 확률분포] 지수분포 (7) 누적분포함수 (0) | 2021.01.18 |
| [손으로 푸는 확률분포] 지수분포 (6) 분산 (0) | 2020.11.23 |
| [손으로 푸는 확률분포] 지수분포 (4) 예시 : 카페 대기시간 (0) | 2020.11.03 |
| [손으로 푸는 확률분포] 지수분포 (3) 예시 : 전자제품 고장확률 (6) | 2020.10.26 |
| [손으로 푸는 확률분포] 지수분포 (2) 유도 (0) | 2020.10.01 |
| [손으로 푸는 확률분포] 지수분포 (1) 소개 (0) | 2020.10.01 |



댓글
bigpicture님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.