지난시간까지 n자유도 카이제곱분포를 유도했습니다. n이 짝수인 경우와, 홀수인 경우를 따로 유도했습니다.
n이 짝수인 경우 카이제곱분포

n이 홀수인 경우 카이제곱분포

오늘은 더블팩토리얼을 변형할건데요. 짝수형부터 변형해보겠습니다. 편하게 유도하기 위해 계수의 분모만 가져다가 유도하겠습니다.
1) 짝수형 변형 (자유도 n이 짝수)
짝수형 수식에서 계수의 분모는 아래와 같습니다.

더블팩토리얼을 전개합시다.

대괄호 안에 있는 인수 개수가 몇개일까요?? 2부터, 짝수 n까지 곱하면 2/n개 입니다. n에서 하나 앞인 n-2까지 곱한 것이므로, 개입니다. 몇개의 숫자를 넣어보면 쉽게 알 수 있습니다. n에 4를 넣어봅시다. 2 이므로, 1개입니다. n에 6을 넣어봅시다. 4x2 이므로 2개입니다. 대괄호 안 인수들에서 2를 꺼내어 아래와 같이 변형합시다.

n이 짝수인 자연수라 괄호 안 인수들은 는 양의 정수이므로, 아래와 같이 팩토리얼 기호를 이용하여 표현할 수 있습니다.

나머지 항들을 계산하면 아래와 같습니다.

따라서 n이 짝수인 경우의 n자유도 카이제곱분포는 아래와 같습니다.

2) 홀수형 변형 (자유도 n이 홀수)
홀수형 수식에서 계수의 분모는 아래와 같습니다.

더블팩토리얼을 전개합시다.

괄호안의 인수는 몇개일까요? 1부터 홀수 n까지 곱하면, (n+1)/2 개입니다. n에서 하나 앞인 n-2까지 곱이므로, 1을 빼면 됩니다. 따라서
개입니다. 몇개의 숫자를 넣어보면 쉽게 알 수 있ㅆ브니다. n에 5를 넣으면 3x1 이므로 인수가 2개입니다. n에 7을 넣으면 5x3x1 이므로 인수가 3개입니다. 대괄호 안의 각 인수에서 2를 꺼내서 아래와 같이 변형합시다.

나머지 항들을 계산하면 아래와 같습니다 .

n이 홀수 이므로, 대괄호 안의 인수들이 자연수가 아닙니다. 예를들어 5를 넣으면, 첫 인수가 2/3 입니다. 문제는 우리가 배운 팩토리얼이 자연수에서만 정의되었다는 것입니다. 3! 이나 10!은 있지만 (1/2)!은 배운적이 없다는 것입니다.
우리에게 필요한 것은 자연수가 아닌 양수에서 정의된 팩토리얼인데요.
자연수가 아닌 양수에서 팩토리얼을 정의할 수는 없을까? 라는 의문을 해결하는 과정에서 등장한 함수가 있습니다.
바로 감마함수입니다. 다음시간에는 감마함수를 배워보고, 홀수형에 적용해보도록 하겠습니다.
현재까지 유도한 함수는 아래와 같습니다.
<짝수형>

<홀수형>
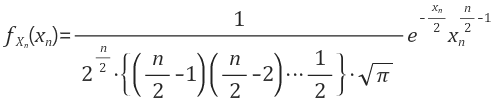
'@ 필수과목 > 손으로 푸는 통계' 카테고리의 다른 글
| [손으로 푸는 통계 ver1.0] 50. 표본분산의 분포 유도 (15) 오일러 극한값의 변형 (0) | 2020.12.21 |
|---|---|
| [손으로 푸는 통계 ver1.0] 49. 표본분산의 분포 유도 (14) 오일러가 발견한 극한값 (0) | 2020.12.15 |
| [손으로 푸는 통계 ver1.0] 48. 표본분산의 분포 유도 (13) 감마함수의 등장 (보완) (0) | 2020.12.14 |
| [손으로 푸는 통계 ver1.0] 47. 표본분산의 분포 유도 (12) 감마함수의 등장 (3) | 2020.08.26 |
| [손으로 푸는 통계 ver1.0] 45. 표본분산의 분포 유도 (10) 카이제곱분포 점화식 풀이 (0) | 2020.06.30 |
| [손으로 푸는 통계 ver1.0] 44. 표본분산의 분포 유도 (9) 1~5자유도 카이제곱분포에서 규칙찾기, 점화식 세우기 (0) | 2020.06.30 |
| [손으로 푸는 통계 ver1.0] 43. 표본분산의 분포 유도 (8) 3,4,5자유도 카이제곱분포 유도 (0) | 2020.06.13 |
| [손으로 푸는 통계 ver1.0] 42. 표본분산의 분포 유도 (7) 2자유도 카이제곱분포 유도 (6) | 2020.05.16 |




댓글
bigpicture님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.