지난시간까지 n자유도 카이제곱분포의 짝수형과 홀수형을 더블팩토리얼형태로 유도하고, 팩토리얼 형태로 변형했습니다. 결과는 아래와 같습니다.
<짝수형>

<홀수형>

짝수형은 팩토리얼 형태로 변형할 수 있었지만, 홀수형은 불가능했습니다. 홀수형의 대괄호안 인수들이 자연수가 아니라 유리수이기 때문입니다. 팩토리얼은 자연수에서만 정의됩니다.
우리는 팩토리얼 개념을 자연수에서 유리수로 확장해야하는 상황입니다.
우리가 알고 있는 팩토리얼의 정의는 아래와 같습니다.

함수 형태로 만들어봅시다. 팩토리얼 함수를 아래와 같이 정의하겠습니다.

왜 f(n)=n! 으로 정의하지 않았냐는 의문이 드는 분도 계실겁니다. n이 자연수이기 때문에 f(n)=n! 으로 정의할 경우 함수값이 1! 부터 시작됩니다. 하지만 팩토리얼은 0! 부터 정의되어 있기 떄문에, 0! 도 함수에 포함시키려는 의도입니다.
이 함수의 한 가지 성질을 도출해봅시다.

위 식을 아래와 같이 변형합니다.

(n-2)! 은 f(n-1) 이므로 아래 수식이 도출됩니다.

한가지 함수를 정의하겠습니다. x가 자연수일 떄는 (x-1)! 이 되고, 자연수가 아닐 때는 f(x)=(x-1)f(x-1) 이라는 성질을 갖는 함수입니다. 이 함수가 바로 감마함수입니다. 감마함수의 수식을 아직 유도하지는 않겠습니다. 일단 위 성질만 이용해서 진행하도록 하겠습니다. 감마함수를 Γ(x) 라고 놓겠습니다.
한가지 의문이 들 수 있습니다. 이 함수가 왜 '감마' 함수가 되었냐는 의문입니다. 감마라는 이름이 붙은 데는 역사적인 이유가 있는데요. 유도할 때 설명하도록 하겠습니다.
Γ(x)의 한가지 예를 들어봅시다. Γ(5)는 무엇일까요? Γ(5)는 4!입니다. 이번에는 정수가 아닌 유리수를 넣어봅시다.
Γ(1/2)는 무엇일까요? 정의를 이용하면 아래와 같이 변형할 수 있습니다.

규칙에 따라 무한히 곱해지는 어떤 값입니다. 이 값이 무엇인지는 위 수식만으로는 구할 수 없습니다. 계산가능한 어떤 수식으로 정의된 감마함수를 찾아야 합니다. 다음시간에 하기로 하고, 오늘은 지금까지 구한 감마함수를 홀수형과 짝수형에 적용해봅시다.
감마 함수를 짝수형에 적용하면, 짝수형은 아래와 같이 표현됩니다.
<짝수형>

이 함수를 홀수형에 적용해봅시다. 홀수형의 대괄호 안 수식은 아래와 같습니다.

감마함수를 이용하여 표현해봅시다. 먼저 Γ(n/2) 을 변형합시다.

홀수형 대괄호 안 수식은 위 빨간부분과 같습니다. 홀수형의 대괄호 안 수식은 아래와 같이 감마함수로 표현될 수 있습니다.

홀수형을 감마함수로 표현하면 아래와 같습니다.
<홀수형>
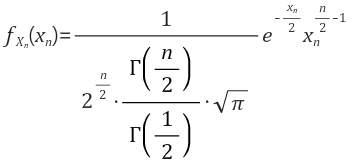
아직도 카이제곱분포가 하나의 수식으로 표현되지는 않네요. 왠지 Γ(1/2) 에 힌트가 있을 것 같습니다. 이 값을 구하려면 감마함수를 수식으로 정의해야하는데요. 다음시간에 해봅시다.
(20201019 다시 보니 설명이 마음에 안든다. f(x)=(x-1)f(x-1) 이 함수가 왜 팩토리얼의 확장인 것인지 설명이 명쾌하지 않다. 팩토리얼에서 매끄러운 interpolation 을 찾고 싶었고, 위 수식을 만족하는 함수가 그에 해당된다는 식으로 설명단계를 구성해야 더 매끄러울듯 하다. 아마 팩토리얼을 포함한 구간에서 연속에 미분가능이라는 것을 보여야 할지도?)
'@ 필수과목 > 손으로 푸는 통계' 카테고리의 다른 글
| [손으로 푸는 통계 ver1.0] 51. 표본분산의 분포 유도 (16) 정의역의 확장 (1) | 2021.03.02 |
|---|---|
| [손으로 푸는 통계 ver1.0] 50. 표본분산의 분포 유도 (15) 오일러 극한값의 변형 (0) | 2020.12.21 |
| [손으로 푸는 통계 ver1.0] 49. 표본분산의 분포 유도 (14) 오일러가 발견한 극한값 (0) | 2020.12.15 |
| [손으로 푸는 통계 ver1.0] 48. 표본분산의 분포 유도 (13) 감마함수의 등장 (보완) (0) | 2020.12.14 |
| [손으로 푸는 통계 ver1.0] 46. 표본분산의 분포 유도 (11) 더블 팩토리얼 변형 (11) | 2020.08.16 |
| [손으로 푸는 통계 ver1.0] 45. 표본분산의 분포 유도 (10) 카이제곱분포 점화식 풀이 (0) | 2020.06.30 |
| [손으로 푸는 통계 ver1.0] 44. 표본분산의 분포 유도 (9) 1~5자유도 카이제곱분포에서 규칙찾기, 점화식 세우기 (0) | 2020.06.30 |
| [손으로 푸는 통계 ver1.0] 43. 표본분산의 분포 유도 (8) 3,4,5자유도 카이제곱분포 유도 (0) | 2020.06.13 |




댓글
bigpicture님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.