지난시간에 배운 내용을 잠깐 리뷰해봅시다.
오일러는 $\frac{1}{2}!=\frac{\sqrt{\pi}}{2}$ 라는 결과에 영감을 받아 팩토리얼이 적분과 관련이 있을 것이라고 생각하게 되고, 아래 적분을 떠올립니다.
$\int_{0}^{1}x^{e}(1-x)^{n}dx$
이 적분식을 지난시간에 아래와 같이 변형했습니다.
$\int_{0}^{1}x^{e}(1-x)^{n}dx= \frac{n!}{(e+1)(e+2)\cdots (e+n)(e+n+1)}$
팩토리얼과 적분을 연결한 식이 유도되었습니다. 오일러는 위 수식을 변형해서 감마함수 적분형을 유도합니다. 유도해보겠습니다.
먼저 $e$ 를 $\frac{f}{g}$ 로 치환합시다.
$\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx= \frac{n!}{(\frac{f}{g}+1)(\frac{f}{g}+2)\cdots (\frac{f}{g}+n)(\frac{f}{g}+n+1)}$
아래와 같이 우변 분모의 각 항을 통분해줍니다.
$\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx= \frac{n!}{
(\frac{f+g}{g})
(\frac{f+2g}{g})\cdots
(\frac{f+ng}{g})
(\frac{f+(n+1)g}{g})
}$
우변을 아래와 같이 변형합시다.
$\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx= \frac{n!}{
\frac{
(f+g)
(f+2g)\cdots
(f+ng)
(f+(n+1)g)
}
{g^{n+1}}
}$
아래와 같이 우변을 둘로 분리해줍니다.
$\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx=
\frac{g^{n+1}}{f+(n+1)g}
\cdot
\frac{n!}{
(f+g)
(f+2g)\cdots
(f+ng)
}$
아래와 같이 우변의 첫항을 좌변으로 옮겨줍니다.
$\frac{f+(n+1)g}{g^{n+1}}
\cdot\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx=
\frac{n!}{
(f+g)
(f+2g)\cdots
(f+ng)
}$
좌우 변을 바꿔줍니다.
$\frac{n!}{
(f+g)
(f+2g)\cdots
(f+ng)
}=
\frac{f+(n+1)g}{g^{n+1}}
\cdot\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx$
치환을 할겁니다. 아래와 같이 치환합니다.
$x=s^{\frac{g}{f+g}}$
$dx=\frac{g}{f+g}s^{-\frac{f}{f+g}}ds$
위 식에 대입합시다.
$\frac{n!}{(f+g)(f+2g) \cdots (f+ng)}=\frac{f+(n+1)g}{g^{n+1}}
\cdot \int_{0}^{1}s^{\frac{f}{f+g}} \left ( 1-s^{ \frac{g}{f+g} } \right )^{n} \frac{g}{f+g}s^{- \frac{f}{f+g}} ds$
아래와 같이 소거합니다.
$\frac{n!}{
(f+g)
(f+2g)\cdots
(f+ng)
}=
\frac{f+(n+1)g}{g^{n+1}}
\cdot\int_{0}^{1}\frac{g}{f+g} \left (1-s^{\frac{g}{f+g}} \right )^{n}ds$
아래와 같이 변형합니다.
$\frac{n!}{
(f+g)
(f+2g)\cdots
(f+ng)
}=
\frac{f+(n+1)g}{g^{n+1}}
\cdot\int_{0}^{1}
\frac{\left ( \frac{g}{f+g} \right )^{n+1}}{\left ( \frac{g}{f+g} \right )^{n}}
\left (1-s^{\frac{g}{f+g}} \right )^{n}ds$
아래와 같이 변형합니다. 적분식 안의 첫 항의 분자는 적분식 바깥의 식과 곱해주고, 분모는 적분식 안의 두번째 항과 합쳐준 것입니다.
$\frac{n!}{(f+g)(f+2g) \cdots (f+ng)}=\frac{f+(n+1)g}{(f+g)^{n+1}}
\cdot \int_{0}^{1} \left ( \frac{1-s^{ \frac{g}{f+g}}}{g/f+g} \right )^{n} ds$
이제 f를 1로 보내고, g를 0으로 보낼 것입니다.
$\lim_{f\rightarrow 1,g\rightarrow 0}\frac{n!}{(f+g)(f+2g) \cdots (f+ng)}=\lim_{f\rightarrow 1,g\rightarrow 0}\frac{f+(n+1)g}{(f+g)^{n+1}}
\cdot \int_{0}^{1} \left ( \frac{1-s^{ \frac{g}{f+g}}}{g/f+g} \right )^{n}ds$
적분안의 항만 따로 계산해봅시다. 아래와 같습니다.
$\lim_{f\rightarrow 1,g\rightarrow 0} \frac{1-s^{ \frac{g}{f+g}}}{g/f+g}$
계산을 편하게 하기 위해 $\frac{g}{f+g}$ 를 z로 치환합시다.
$\lim_{z\rightarrow 0} \frac{1-s^{z}}{z}$
로피탈 정리를 이용하여 극한값을 구하겠습니다. 분자와 분모를 z로 미분합니다. $(a^{x})'=\ln a \cdot a^{x}$ 를 이용합니다.
$\lim_{z\rightarrow 0} \frac{1-s^{z}}{z}=\lim_{z\rightarrow 0} \frac{-\ln s \cdot s^{z}}{1}=-\ln s$
우리가 계산하던 식을 다시 가져옵시다.
$\lim_{f\rightarrow 1,g\rightarrow 0}\frac{n!}{(f+g)(f+2g) \cdots (f+ng)}=\lim_{f\rightarrow 1,g\rightarrow 0}\frac{f+(n+1)g}{(f+g)^{n+1}}
\cdot \int_{0}^{1} \left ( \frac{1-s^{ \frac{g}{f+g}}}{g/f+g} \right )^{n}ds$
극한값은 아래와 같습니다.
$n!=\int_{0}^{1} \left ( -\ln s \right )^{n}dt$
치환을 하겠습니다. $-\ln s $를 t로 치환합시다.
$\begin{align}
-\ln s &=t \\
s&=e^{-t} \\
ds&=-e^{-t}dt
\end{align}$
적분범위를 구하기 위해 그래프를 그리면 아래와 같습니다.
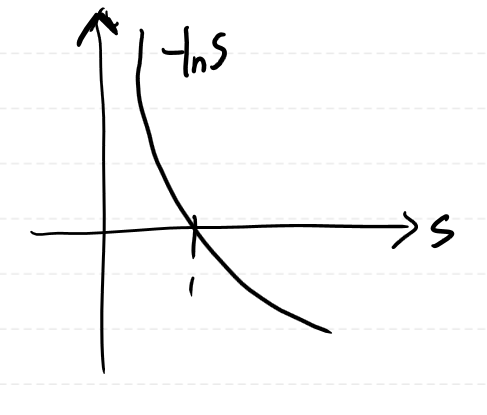
s가 0에서 1로 변할 때, t는 무한대에서 0으로 변합니다.
$n!=\int_{\infty}^{0}t^{n}(-e^{-t})dt$
아래와 같이 변형합시다. 적분구간을 뒤집으면 부호가 바뀝니다.
$n!=\int_{0}^{\infty}t^{n}e^{-t}dt$
감마함수는 팩토리얼함수에서 정의역을 확장한 것이므로 n대신 n-1을 넣어서 팩토리얼 함수로 만들어줍니다.
$(n-1)!=\int_{0}^{\infty}t^{n-1}e^{-t}dt$
n을 실수 영역으로 확장하면 감마함수가 됩니다.
$\Gamma (z)=\int_{0}^{\infty}t^{z-1}e^{-t}dt$
'@ 필수과목 > 손으로 푸는 통계' 카테고리의 다른 글
| [손으로 푸는 통계 ver1.0] 66. 표본분산의 분포 유도 (31) 감마함수 수렴성 증명 #2 (0) | 2021.09.18 |
|---|---|
| [손으로 푸는 통계 ver1.0] 65. 표본분산의 분포 유도 (30) 감마함수 수렴성 증명 #1 (0) | 2021.08.01 |
| [손으로 푸는 통계 ver1.0] 64. 표본분산의 분포 유도 (29) 감마 1/2 계산하기 (0) | 2021.08.01 |
| [손으로 푸는 통계 ver1.0] 63. 표본분산의 분포 유도 (28) 감마함수 적분형의 재귀적 성질 (0) | 2021.08.01 |
| [손으로 푸는 통계 ver1.0] 61. 표본분산의 분포 유도 (26) 팩토리얼과 적분의 연결 (0) | 2021.06.19 |
| [손으로 푸는 통계 ver1.0] 60. 표본분산의 분포 유도 (25) 이분의일 팩토리얼이 이분의 루트 파이임을 증명 (0) | 2021.06.19 |
| [손으로 푸는 통계 ver1.0] 59. 표본분산의 분포 유도 (24) 왈리스 공식 유도3 (Wallis product) (0) | 2021.06.19 |
| [손으로 푸는 통계 ver1.0] 58. 표본분산의 분포 유도 (23) 왈리스 공식 유도2 (Wallis product) (0) | 2021.06.12 |
댓글