[손으로 푸는 통계 ver1.0] 62. 표본분산의 분포 유도 (27) 감마함수 적분형 유도

 

 

지난시간에 배운 내용을 잠깐 리뷰해봅시다. 

 

오일러는 $\frac{1}{2}!=\frac{\sqrt{\pi}}{2}$ 라는 결과에 영감을 받아 팩토리얼이 적분과 관련이 있을 것이라고 생각하게 되고, 아래 적분을 떠올립니다. 

 

$\int_{0}^{1}x^{e}(1-x)^{n}dx$

 

이 적분식을 지난시간에 아래와 같이 변형했습니다. 

 

$\int_{0}^{1}x^{e}(1-x)^{n}dx= \frac{n!}{(e+1)(e+2)\cdots (e+n)(e+n+1)}$

 

팩토리얼과 적분을 연결한 식이 유도되었습니다. 오일러는 위 수식을 변형해서 감마함수 적분형을 유도합니다. 유도해보겠습니다. 

 

먼저 $e$ 를 $\frac{f}{g}$ 로 치환합시다. 

 

$\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx= \frac{n!}{(\frac{f}{g}+1)(\frac{f}{g}+2)\cdots (\frac{f}{g}+n)(\frac{f}{g}+n+1)}$

 

아래와 같이 우변 분모의 각 항을 통분해줍니다. 

 

$\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx= \frac{n!}{
(\frac{f+g}{g})
(\frac{f+2g}{g})\cdots 
(\frac{f+ng}{g})
(\frac{f+(n+1)g}{g})
}$

 

우변을 아래와 같이 변형합시다. 

 

$\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx= \frac{n!}{
\frac{
(f+g)
(f+2g)\cdots 
(f+ng)
(f+(n+1)g)
}
{g^{n+1}}
}$

 

아래와 같이 우변을 둘로 분리해줍니다. 

 

$\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx= 
\frac{g^{n+1}}{f+(n+1)g}
\cdot
\frac{n!}{
(f+g)
(f+2g)\cdots 
(f+ng)
}$

 

아래와 같이 우변의 첫항을 좌변으로 옮겨줍니다. 

 

$\frac{f+(n+1)g}{g^{n+1}}
\cdot\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx= 
\frac{n!}{
(f+g)
(f+2g)\cdots 
(f+ng)
}$

 

좌우 변을 바꿔줍니다. 

 

$\frac{n!}{
(f+g)
(f+2g)\cdots 
(f+ng)
}=
\frac{f+(n+1)g}{g^{n+1}}
\cdot\int_{0}^{1}x^{\frac{f}{g}}(1-x)^{n}dx$

 

치환을 할겁니다. 아래와 같이 치환합니다. 

 

$x=s^{\frac{g}{f+g}}$ 

 

$dx=\frac{g}{f+g}s^{-\frac{f}{f+g}}ds$

 

위 식에 대입합시다. 

 

$\frac{n!}{(f+g)(f+2g) \cdots (f+ng)}=\frac{f+(n+1)g}{g^{n+1}}
\cdot \int_{0}^{1}s^{\frac{f}{f+g}} \left ( 1-s^{ \frac{g}{f+g} } \right )^{n} \frac{g}{f+g}s^{- \frac{f}{f+g}} ds$

 

아래와 같이 소거합니다. 

 

$\frac{n!}{
(f+g)
(f+2g)\cdots 
(f+ng)
}=
\frac{f+(n+1)g}{g^{n+1}}
\cdot\int_{0}^{1}\frac{g}{f+g} \left (1-s^{\frac{g}{f+g}} \right )^{n}ds$

 

아래와 같이 변형합니다. 

 

$\frac{n!}{
(f+g)
(f+2g)\cdots 
(f+ng)
}=
\frac{f+(n+1)g}{g^{n+1}}
\cdot\int_{0}^{1}
\frac{\left ( \frac{g}{f+g} \right )^{n+1}}{\left ( \frac{g}{f+g} \right )^{n}} 
\left (1-s^{\frac{g}{f+g}} \right )^{n}ds$

 

아래와 같이 변형합니다. 적분식 안의 첫 항의 분자는 적분식 바깥의 식과 곱해주고, 분모는 적분식 안의 두번째 항과 합쳐준 것입니다. 

 

$\frac{n!}{(f+g)(f+2g) \cdots (f+ng)}=\frac{f+(n+1)g}{(f+g)^{n+1}}
\cdot \int_{0}^{1} \left ( \frac{1-s^{ \frac{g}{f+g}}}{g/f+g} \right )^{n}  ds$

 

이제 f를 1로 보내고, g를 0으로 보낼 것입니다. 

 

$\lim_{f\rightarrow 1,g\rightarrow 0}\frac{n!}{(f+g)(f+2g) \cdots (f+ng)}=\lim_{f\rightarrow 1,g\rightarrow 0}\frac{f+(n+1)g}{(f+g)^{n+1}}
\cdot \int_{0}^{1} \left ( \frac{1-s^{ \frac{g}{f+g}}}{g/f+g} \right )^{n}ds$

 

적분안의 항만 따로 계산해봅시다. 아래와 같습니다. 

 

$\lim_{f\rightarrow 1,g\rightarrow 0} \frac{1-s^{ \frac{g}{f+g}}}{g/f+g}$

 

계산을 편하게 하기 위해 $\frac{g}{f+g}$ 를 z로 치환합시다. 

 

$\lim_{z\rightarrow 0} \frac{1-s^{z}}{z}$

 

로피탈 정리를 이용하여 극한값을 구하겠습니다. 분자와 분모를 z로 미분합니다. $(a^{x})'=\ln a \cdot a^{x}$ 를 이용합니다. 

 

$\lim_{z\rightarrow 0} \frac{1-s^{z}}{z}=\lim_{z\rightarrow 0} \frac{-\ln s \cdot s^{z}}{1}=-\ln s$

 

우리가 계산하던 식을 다시 가져옵시다. 

 

$\lim_{f\rightarrow 1,g\rightarrow 0}\frac{n!}{(f+g)(f+2g) \cdots (f+ng)}=\lim_{f\rightarrow 1,g\rightarrow 0}\frac{f+(n+1)g}{(f+g)^{n+1}}
\cdot \int_{0}^{1} \left ( \frac{1-s^{ \frac{g}{f+g}}}{g/f+g} \right )^{n}ds$

 

극한값은 아래와 같습니다. 

 

$n!=\int_{0}^{1} \left ( -\ln s \right )^{n}dt$

 

치환을 하겠습니다. $-\ln s $를 t로 치환합시다. 

 

$\begin{align}
-\ln s &=t \\
s&=e^{-t} \\
ds&=-e^{-t}dt
\end{align}$

 

적분범위를 구하기 위해 그래프를 그리면 아래와 같습니다. 

 

 

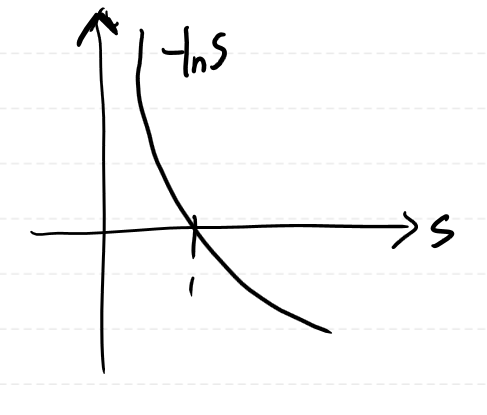
s가 0에서 1로 변할 때, t는 무한대에서 0으로 변합니다. 

 

$n!=\int_{\infty}^{0}t^{n}(-e^{-t})dt$

 

아래와 같이 변형합시다. 적분구간을 뒤집으면 부호가 바뀝니다. 

 

$n!=\int_{0}^{\infty}t^{n}e^{-t}dt$

 

감마함수는 팩토리얼함수에서 정의역을 확장한 것이므로 n대신 n-1을 넣어서 팩토리얼 함수로 만들어줍니다. 

 

$(n-1)!=\int_{0}^{\infty}t^{n-1}e^{-t}dt$

 

n을 실수 영역으로 확장하면 감마함수가 됩니다. 

 

$\Gamma (z)=\int_{0}^{\infty}t^{z-1}e^{-t}dt$