우리는 지금까지 이산확률분포들을 배웠습니다. 아래의 7가지 분포입니다.
- 베르누이분포
- 이항분포
- 기하분포
- 음이항분포
- 포아송분포
- 초기하분포
- 다항분포
이번 글에서는 각 분포들 사이의 관계망을 만들어보도록 하겠습니다.
베르누이분포로 시작합니다. 베르누이분포는 시행횟수가 1회이고, 시행의 결과가 성공/실패 둘 뿐인 분포입니다. 분포함수는 아래와 같습니다. 기호로는 B(1,p)로 나타냅니다.

베르누이분포에서 시행횟수를 n회로 늘리면 이항분포가 됩니다. 기호로는 B(n,p)로 나타냅니다.

이항분포에서 시행의 결과로 발생하는 사건의 종류를 늘리면 다항분포가 됩니다. 기호로는 M(n,p1,p2,...)로 나타냅니다.

이항분포에서 시행횟수를 무한대로 보내고, 사건 발생확률을 0으로 보내면 푸아송분포가 됩니다. 기호로는 Pois(λ) 로 나타냅니다.

이항분포에서 복원추출을 비복원추출로 바꾸면 초기하분포가 됩니다. 반대로 초기하분포에서 시행횟수 M을 무한대로 보내면 이항분포에 가까워져 갑니다. Hyp(M,n,k)로 나타냅니다.

몇개남았죠? - 베르누이분포
- 이항분포
- 기하분포
- 음이항분포
- 포아송분포
- 초기하분포
- 다항분포
음이항분포는 r번의 실패가 나오기까지 발생한 성공이 x번일 확률분포입니다. 기호로는 NB(r,p)라고 나타냅니다.

음이항분포는 푸아송분포와 관계를 갖습니다. 음이항분포에서 r이 무한대로 가고, p가 1에 가까워 가면 음이항분포는 푸아송분포에 가까워져 갑니다. 이때 λ 는 n(1-p) 입니다. 이 내용은 이전 강의에서 다루지 않았습니다. 시즌2에서 다루도록 하겠습니다.

음이항분포에서 r이 1이면 기하분포가 됩니다.

수식이 달라서 헷갈리실 수 있어 추가설명을 하겠습니다. 위 음이항분포 수식에서, r에 1을 넣으면 아래와 같습니다.
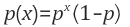
기하분포 수식과 달라보이는데, 의미를 생각해보면 같다는 것을 알 수 있습니다. 위 식은 실패가 나오기 까지, x번의 성공이 발생할 확률입니다.
기하분포의 수식은 처음 성공이 나오기까지 시행한 횟수가 x번일 확률입니다. 다른 말로 하면 성공이 나오기 까지 x-1번의 실패가 발생할 확률인 것입니다. 의미가 같다는 것을 알 수 있습니다.
'@ 필수과목 > 손으로 푸는 확률분포' 카테고리의 다른 글
| [손으로 푸는 확률분포] 지수분포 (1) 소개 (0) | 2020.10.01 |
|---|---|
| [손으로 푸는 확률분포] 균등분포 (3) 예시 (0) | 2020.02.29 |
| [손으로 푸는 확률분포] 균등분포 (2) 평균과 분산 (1) | 2020.02.26 |
| [손으로 푸는 확률분포] 균등분포 (1) 소개,그래프,유도 (2) | 2020.02.24 |
| [손으로 푸는 확률분포] 이산확률분포 7가지 총정리 (0) | 2020.02.18 |
| [손으로 푸는 확률분포] 다항분포 (6) 그래프 (2) | 2020.02.15 |
| [손으로 푸는 확률분포] 다항분포 (5) 독립변수의 개수 (0) | 2020.02.11 |
| [손으로 푸는 확률분포] 다항분포 (4) 평균과 분산 (2) | 2020.02.07 |




댓글
bigpicture님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.