[손으로 푸는 통계] 15. 정규분포 함수 유도 (방법1. 과녁맞추기를 이용한 유도 1/2)

정규분포 함수 유도 (방법1. 과녁맞추기를 이용한 유도 1/2)

지난 세 강에 걸쳐서 표본의 크기 n이 충분히 클 때 표본평균의 분포가 정규분포를 따른다는 것을 유도했습니다. 정규분포는 당연히 알고 있다는 듯 사용했지만, 우리는 정규분포가 어디에서 왔는지 모릅니다. 

정규분포함수는 고등학교 확률과 통계시간에 처음 배웠던걸로 기억합니다. 고등학교 시절 정규분포를 접했을 때, 도데체 이 함수가 어디서 온 것인지 궁금했었습니다. 정규분포가 우리 주변에 여러곳에서 발견된다는 이야기를 듣고, 이와 비슷한 모양의 함수를 찾은 것인가 생각하기도 했습니다. 언젠가 꼭 이유를 밝혀보고 싶다는 생각을 갖고 있었는데요. 우연히 통계 유튜브와 블로그를 시작하게 됐고, 결국 궁금증을 해결할 수 있었습니다. 

제가 찾은 정규분포 유도 방법은 두 가지 입니다. 

- 과격 맞추기를 이용한 유도
- 이항분포를 이용한 유도

두 유도방법 모두 정규분포가 무엇인가에 대한 통찰을 제공합니다. 먼저 각 방법으로 유도 하고 나서, 정규분포의 의미에 대한 이야기를 해보도록 합시다. 

 

과녁맞추기를 이용한 유도 (1/2)

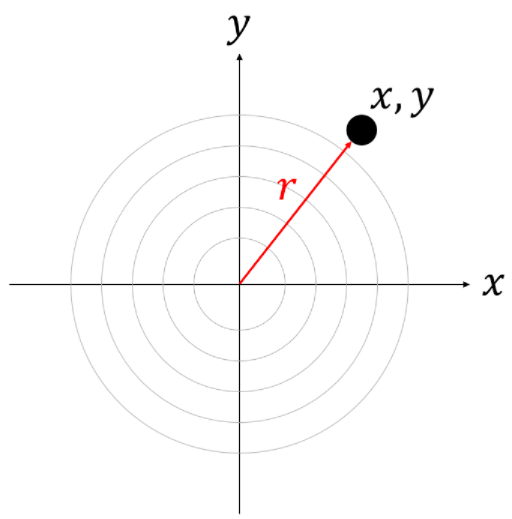
아래 그림처럼 xy 평면에 과녁이 하나 놓여있다고 합시다. 

 

우리가 화살쏘기에 숙련된 전문가라고 가정합시다. 중앙을 겨냥해서 화살을 쏠 것입니다. 아무리 전문가라고 해도 항상 과녁 중앙에 화살을 맞출 수는 없습니다. 아래 그림 처럼 화살이 빗나가는 경우도 있을 것입니다. 

 

이 상황을 확률분포로 만들어봅시다. 확률분포로 만들기 위해 두가지 가정을 하겠습니다. 

 

1) 과녁의 중심에서 멀어질 수록 맞출 확률이 낮다. 

2) 과녁의 중심에서 거리가 같은 두 점이 있다면, 이 두 점의 확률은 동일하다. 

 

과녁 위 어느 한 점에 맞을 확률을 생각해봅시다. 확률변수는 $X$와 $Y$입니다. 확률은 $P(x,y)$로 정의될 텐데요. X와 Y가 연속확률변수이므로, 확률밀도함수를 갖습니다. $f(x,y)$라고 놓겠습니다. $f(x\cap y)$ 와 같은 의미입니다. 

 

확률밀도함수를 전체 구간(도메인)에 대해 적분한 값은 1입니다. 따라서 아래 등식이 성립합니다. 

 

$\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }f(x,y)dxdy=1$

 

x의 주변확률분포

확률밀도함수 $f(x,y)$를 y의 전체구간에 대해 적분해봅시다. 

 

$\int_{-\infty }^{\infty }f(x,y)dy$

 

y에 대해 정적분을 한 것이므로, 결과는 x만의 함수가 됩니다. 계산 결과를 $f_{x}(x)$ 라고 놓겠습니다.

 

$\int_{-\infty }^{\infty }f(x,y)dy=f_{x}(x)$

 

x의 주변확률분포라고 합니다. 이 함수의 의미를 생각해봅시다. x에 어떤 값 a를 대입해봅시다. $f_{x}(a)$인데요. $f_{x}(a)$는 아래 그림과 같이 $x=a$ 인 선 위에 화살이 맞을 확률밀도를 의미합니다. 

 

 

y의 주변확률분포

확률밀도함수 $f(x,y)$를 x의 전체구간에 대해 적분해봅시다. 

 

$\int_{-\infty }^{\infty }f(x,y)dx$

 

x에 대해 정적분을 한 것이므로, 결과는 y만의 함수가 됩니다. 계산 결과를 $f_{y}(y)$ 라고 놓겠습니다.

 

$\int_{-\infty }^{\infty }f(x,y)dx=f_{y}(y)$

 

y의 주변확률분포라고 합니다. 이 함수의 의미를 생각해봅시다. y에 어떤 값 a를 대입해봅시다. $f_{y}(a)$인데요. $f_{y}(a)$는 $y=a$ 인 선 위에 화살이 맞을 확률밀도를 의미합니다. 

 

원점으로 부터의 거리에 따라 확률이 변한다고 가정했기 때문에, x방향으로 멀어지는 것과 y방향으로 멀어지는 것의 영향이 동일합니다. 따라서 $f_{x}(x)$ 와 $f_{y}(y)$ 는 동일한 함수입니다. 앞으로는 아래첨자를 생략하고 $f(x),f(y)$ 라고 놓겠습니다. 

 

 

독립성 가정

한가지 가정을 추가합시다. 확률변수 x와 y가 서로 독립이라는 가정입니다. 독립성 가정에 의해 아래 등식이 성립합니다. (참고: hsm-edu.tistory.com/1178?category=770915)

 

$f(x,y)=f(x\cap y)=f(x)f(y)$

 

화살을 쏘는 상황에서 두 확률변수가 독립이라는 것을 직관적으로 어떻게 이해할 수 있는가 생각해보는 것도 흥미로운 주제입니다. 다루지는 않겠지만 한번 고민해봅시다. 

 

 

거리가 r인 곳의 확률밀도 함수

함수를 하나 더 정의하겠습니다. 과녁의 중심에서 부터 거리가 $r$인 곳의 확률밀도를 $g(r)$ 이라고 놓겠습니다. 여기서 주의할 점은 $g(r)$이 거리가 r인 어느 한 지점의 확률밀도라는 것입니다. 거리가 r인 지점들의 자취인 '원'의 확률밀도가 아닙니다. 원점에서 부터의 거리가 $r$인 어떤 좌표를 $(x,y)$라고 놓는다면 아래 등식이 성립합니다.

 

$g(r)=f(x,y)$

 

 

확률변수 x,y가 서로 독립이므로 아래 등식이 성립합니다. 

 

$g(r)=f(x)f(y)$

 

이때 x축과 r방향 사이의 각도를 $\theta$ 라고 놓는다면 x와 y를 아래와 같이 나타낼 수 있습니다. 

 

$x=rcos(\theta)$

$y=rsin(\theta)$

 

$g(r)=f(x)f(y)$ 식의 양변을 $\theta$로 미분하겠습니다. $g(r)$은 $\theta$와 무관한 함수이므로 미분하면 0이 됩니다. 

 

$0=\frac{df(x)}{d\theta}f(y)+f(x)\frac{df(y)}{d\theta}$

 

체인룰을 적용합시다.

 

$0=\frac{df(x)}{dx}\frac{dx}{d\theta} f(y)+f(x)\frac{df(y)}{dy}\frac{dy}{d\theta}$

 

아래와 같이 변형합시다.

 

$0=f'(x)\frac{dx}{d\theta} f(y)+f(x)f'(y)\frac{dy}{d\theta}$

 

아래와 같이 $\theta$로 미분된 항에 있는 $x$와 $y$를 $r$과 $\theta$에 대한 식으로 바꿔줍니다. 

 

$0=f'(x)\frac{drcos(\theta)}{d\theta} f(y)+f(x)f'(y)\frac{drsin(\theta)}{d\theta}$

 

$\theta$로 미분합시다.

 

$0=f'(x)(-rsin\theta) f(y)+f(x)f'(y)(rcos\theta)$

 

아래와 같이 양변을 정리합시다.

 

$\frac{f'(x)}{f(x)}\frac{rsin\theta}{rcos\theta}=\frac{f'(y)}{f(y)}$

 

r을 약분합시다. 

 

$\frac{f'(x)}{f(x)}\frac{sin\theta}{cos\theta}=\frac{f'(y)}{f(y)}$

 

$\frac{sin\theta}{cos\theta}$는 $tan\theta$이므로 아래와 같이 변형합시다. 

 

$\frac{f'(x)}{f(x)}tan\theta=\frac{f'(y)}{f(y)}$

 

$tan\theta$ 는 $\frac{y}{x}$이므로 아래와 같이 변형할 수 있습니다. 

 

$\frac{f'(x)}{f(x)}\frac{y}{x}=\frac{f'(y)}{f(y)}$

 

$y$로 양변을 나눠줍시다. 

 

$\frac{f'(x)}{f(x)}\frac{1}{x}=\frac{f'(y)}{f(y)}\frac{1}{y}$

 

x와 y에는 모든 실수가 올 수 있기 때문에, 어떤 값을 넣어도 위 등식이 성립한다는 의미입니다. 만약 좌변이 x에 대한 변수이고, 우변이 y에 대한 변수라면 등식이 성립하지 않는 경우가 존재하게 됩니다. 따라서 좌변과 우변은 상수입니다.

 

$\frac{f'(x)}{f(x)}\frac{1}{x}=\frac{f'(y)}{f(y)}\frac{1}{y}=C$

 

x에 대해서만 생각해봅시다. 아래 등식입니다. 

 

$\frac{f'(x)}{f(x)}\frac{1}{x}=C$

 

양변에 x를 곱해줍시다.

 

$\frac{f'(x)}{f(x)}=Cx$

 

양변을 x에 대해 적분합시다.

 

$\mathrm{ln}f(x)=\frac{1}{2}Cx^{2}+D$

 

f(x)에 대해 정리하면 아래와 같습니다. 

 

$f(x)=e^{\frac{C}{2}x^{2}}e^{D}$

 

$e^{D}$는 상수이므로, 상수 A로 간단히 표현하겠습니다. 

 

$f(x)=Ae^{\frac{C}{2}x^{2}}$

 

다음시간에는 상수 A와 C를 구해봅시다. 

 

#강의 영상