[손으로 푸는 통계] 24. 통계적 가설 검정 감잡기 4 (양측검정 vs 단측검정)

우리는 지난시간까지 아래 내용을 배운 상태입니다. 

- 귀무가설, 대립가설
- 가설검정 원리
- 유의수준 ($\alpha$)

- 유의확률 (p-value)

 

이번시간에는 기각역, 양측검정, 단측검정을 배워봅시다. 지난시간에 사용한 예시를 가져옵시다. 모집단이 하나 있는데, 평균이 $\mu$라고 알려져 있습니다. 우리는 이 주장에 반대하는 상황입니다. Z검정을 하기 위해 귀무가설과 대립가설을 아래와 같이 세웠습니다. 

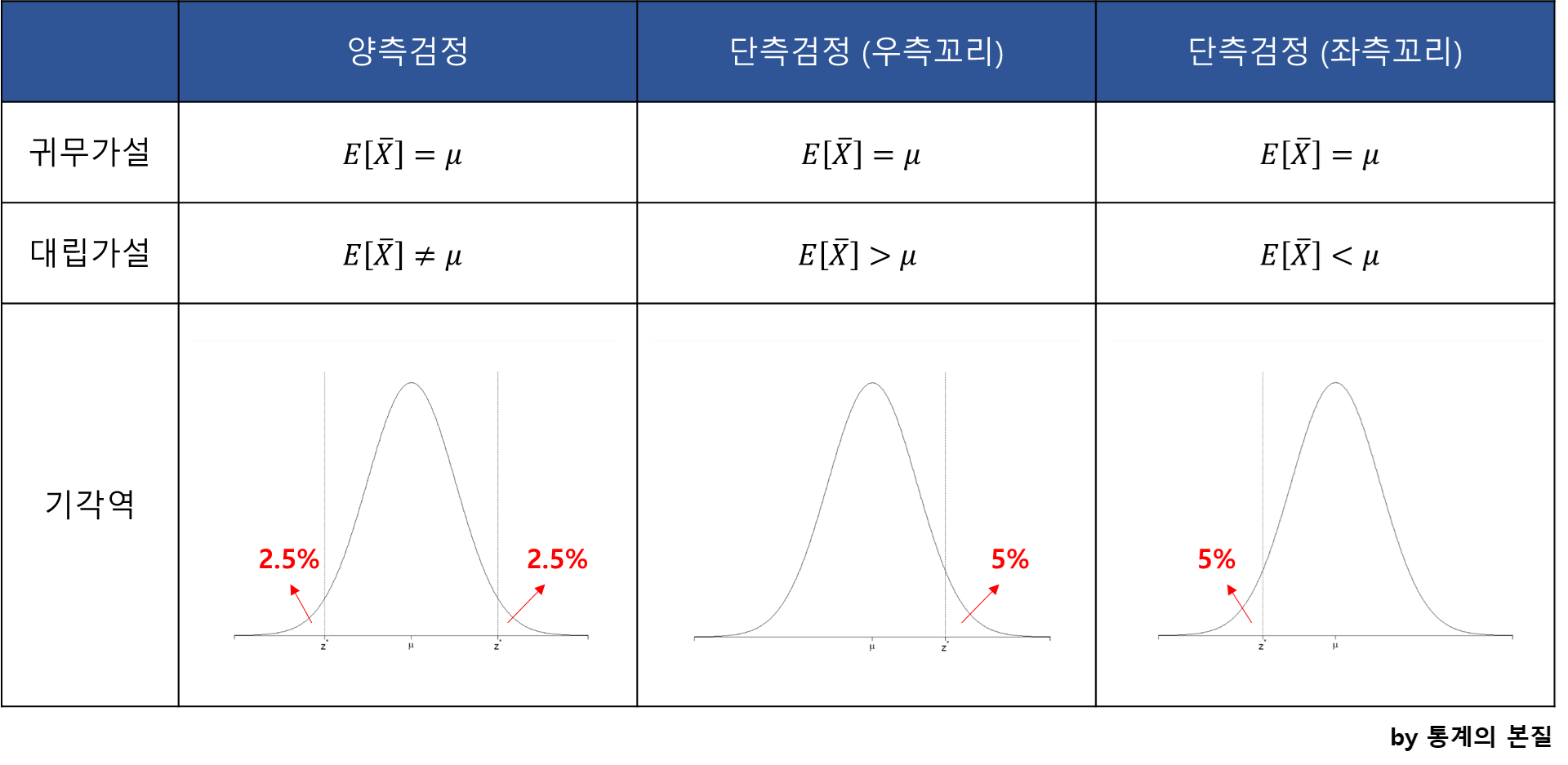
귀무가설 : $E[\bar{X}]=\mu$ (기존의 주장)
대립가설 : $E[\bar{X}] \neq \mu$ (기존의 주장에 반대하는 우리의 주장)

 

이 모집단에서 표본을 하나 뽑아서 평균을 구했습니다. 우리가 뽑은 표본의 평균을 $\bar{X}_{1}$ 라고 합시다. $\bar{X}_{1}$ 보다 극단적인 값이 뽑힐 확률을 구했더니 0.1%가 나왔습니다. 그림으로 나타내면 아래와 같습니다. 

 

 

이 확률을 유의확률이라고 합니다. 유의확률이 몇 % 이하일 경우 귀무가설을 기각시킬지 정해야 하는데요. 일반적으로 5%를 사용한다고 이야기했습니다. 기각의 기준이 되는 5%를 유의수준이라고 부릅니다. 

 

양측검정

그런데 여기서 한가지 생각해볼 문제가 있습니다. 위 경우는 우리가 구한 표본평균이 $\mu$보다 지나치게 크게 나왔기 때문에 모평균이 $\mu$라는 주장을 기각하는 것입니다. 반대로 우리가 구한 표본평균이 모평균보다 지나치게 작게 나와도 귀무가설은 기각될 수 있습니다. 따라서 기각되는 영역이 양쪽 끝에 존재하는 것입니다. 우리는 5%를 이하를 기각하려고 한 것이므로, 한쪽에 2.5%씩을 기각하는 영역으로 놓아야 합니다. 그림으로 나타내면 아래와 같습니다. 

 

우리가 뽑은 표본평균이 이 영역 안에 들어오면 귀무가설을 기각합니다. 이 영역을 '기각역'이라고 부릅니다. 위와 같이 기각역이 양쪽에 있는 경우를 '양측 검정'이라고 합니다. 영어로는 two-tailed test 라고 합니다. 꼬리가 양쪽에 있다는 의미입니다. 

 

양측검정의 귀무가설은 아래와 같습니다. 

귀무가설 : $E[\bar{X}]=\mu$ (기존의 주장)
대립가설 : $E[\bar{X}] \neq \mu$ (기존의 주장에 반대하는 우리의 주장)

 

단측검정

기각역이 한쪽에만 있는 '단측검정'도 존재합니다. 모평균이 $\mu$과 다르다고 주장하는게 아니라, 모평균이 $\mu$ 보다 크다고 주장하는 경우입니다. 귀무가설과 대립가설은 아래와 같습니다. 

귀무가설 : $E[\bar{X}]=\mu$ (기존의 주장)
대립가설 : $E[\bar{X}] > \mu$ (기존의 주장에 반대하는 우리의 주장)

 

이런 경우에는 표본평균의 평균이 분포의 우측 극단에 있는 경우에만 귀무가설을 기각하고 대립가설을 채택할 수 있습니다. 따라서 기각역은 아래와 같습니다. 단측검정은 영어로 one-tailed test 입니다. 꼬리가 하나라는 뜻입니다. 

 

 

만약 대립가설이 $E[\bar{X}] < \mu$ 라면 기각역은 좌측꼬리에 존재합니다. 

 

단측검정과 양측검정의 차이를 표로 요약하면 아래와 같습니다. 

 

 

#영상 강의