아래는 지난시간에 그렸던 그래프입니다. 1~10의 자연수를 갖는 모집단에서 크기가 30인 표본을 뽑고, 표본분산의 분포를 그래프로 그린 것입니다. 더 정확히 말하면 아래 확률변수의 분포입니다.
오른쪽 그림은 29자유도의 카이제곱분포입니다. n이 커지면 표본분산의 그래프는 n-1 자유도 카이제곱분포를 따른다고 알려져 있습니다.

나란히 그려진 상태에서 보니 비슷해 보였는데요. 그래프를 겹쳐서 그려보니 이야기가 달라졌습니다.

많이 다릅니다. 겹쳐 그린 그래프로 다시 시뮬레이션을 해보려고 합니다. 모집단을 더 다양화했고 절차도 가다듬었습니다.
1. 배경
우리가 표본분산의 분포를 유도할 때 설정했던 두 가지 조건은 아래와 같습니다.
1) 표본평균의 분포가 정규분포를 따를 만큼 표본의 크기 n이 크다.
2) 모집단의 분포는 정규분포를 따른다.
1번은 표본의 크기를 충분히 크게 하면 되는거구요. 두번째 조건도 표본의 크기가 충분히 크면 무시할 수 있다는 것을 지난시간에 다뤘습니다. 증명하진 않고 증명이 되어 있는 논문만 보여드렸습니다.
오늘은 통계 프로그램인 R을 이용해서 정말 표본의 크기가 충분히 크면 모집단이 정규분포를 따르지 않아도 표본분산이 카이제곱분포를 따르는지 확인해보려고 합니다.
2.변수
모집단와 표본을 바꿔가며 표본분산의 분포가 카이제곱분포를 따르는지 확인해볼 것입니다.
모집단은 네 가지 종류로 설정했습니다.
모집단1 : 1~10 의 자연수. 1:10으로 표기
모집단2 : 1~1000 의 자연수. 1:1000으로 표기
모집단3 : 표준정규분포에서 추출한 10개의 값
모집단4 : 표준정규분포에서 추출한 1000개의 값
표본의 크기는 3,30,50,100,1000,3000 으로 설정하였습니다.
3.실험 방법
모집단 1에서 크기 30인 표본을 뽑는 경우를 예로 들겠습니다. 모집단 1에서 크기 30인 표본을 10000개 뽑습니다. 각 표본에 대해 아래 통계량을 계산합니다.
10000개의 값이 생겼습니다. 이 값들로 히스토그램을 그립니다. 표본의 크기가 30이면, 29자유도 카이제곱분포를 따른다고 가정할 수 있습니다. 아래와 같이 두 그래프를 겹쳐 그려서 비교합니다.

4.결과
결과를 표로 정리하였습니다.
4-1) 모집단1 (1:10)
모집단 1:10 에서 표본을 추출하여 그린 그래프입니다. 모양은 비슷하지만 값이 많이 다른 것을 알 수 있습니다. 실제 분포함수 보다 카이제곱분포가 더 분산이 큽니다. 표본이 커져도 두 분포가 같아지지 않습니다. 우측 꼬리 검정이나 좌측꼬리 검정을 하면 p값이 상당히 차이날 것으로 생각됩니다. 아주 단순한 모집단을 가정한 것이라 실제 이런 경우는 없겠지만, 모집단의 분포와 상관 없이 표본의 크기가 커지면 카이제곱분포로 가정할 수 있다는 이론이 잘 맞지는 않네요.

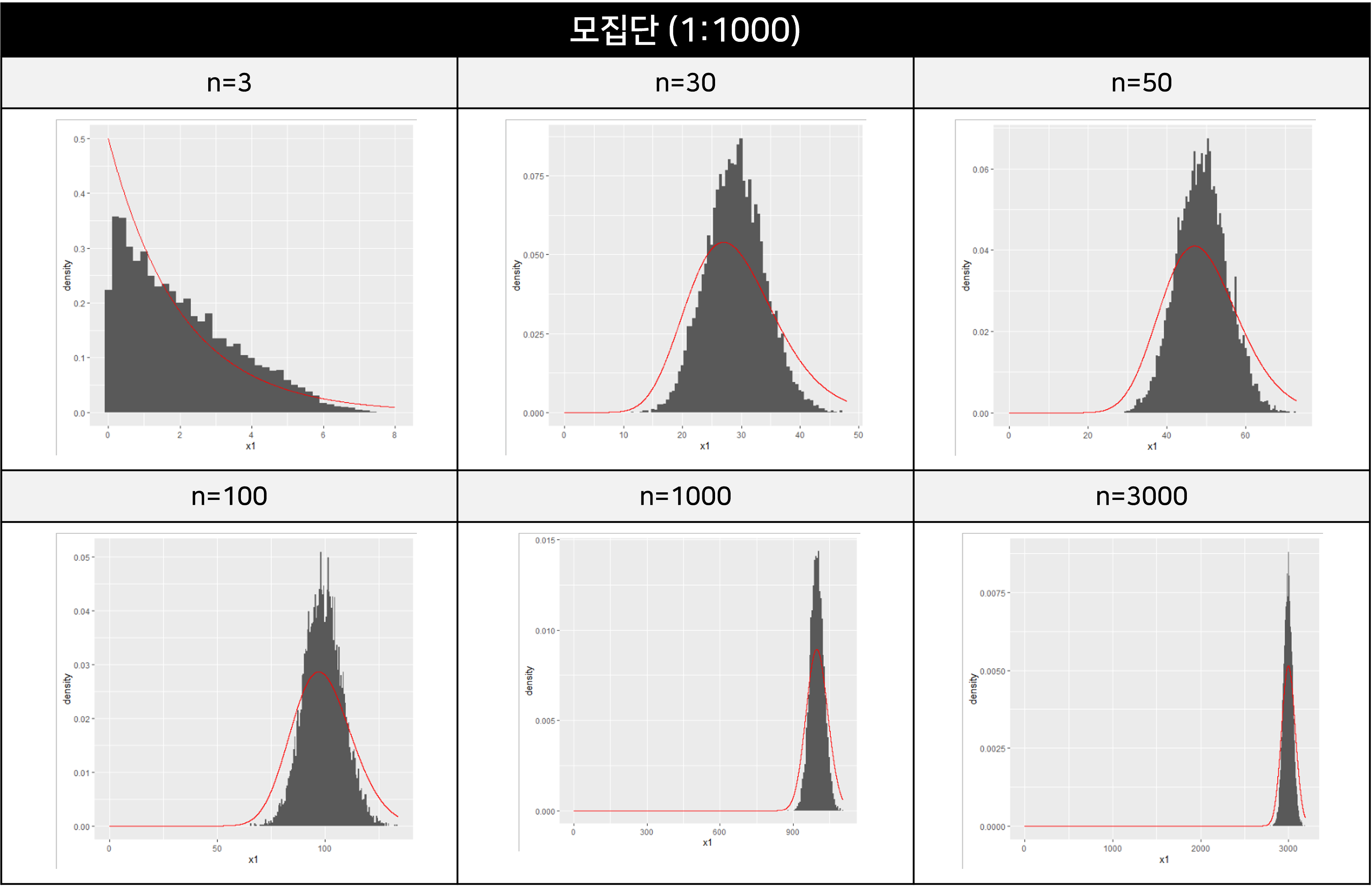
4-2) 모집단2 (1:1000)
모집단 1처럼 균등분포입니다. 범위가 개수를 늘렸습니다. 결과는 모집단 1과 비슷합니다. 카이제곱분포와 일치하지 않습니다.
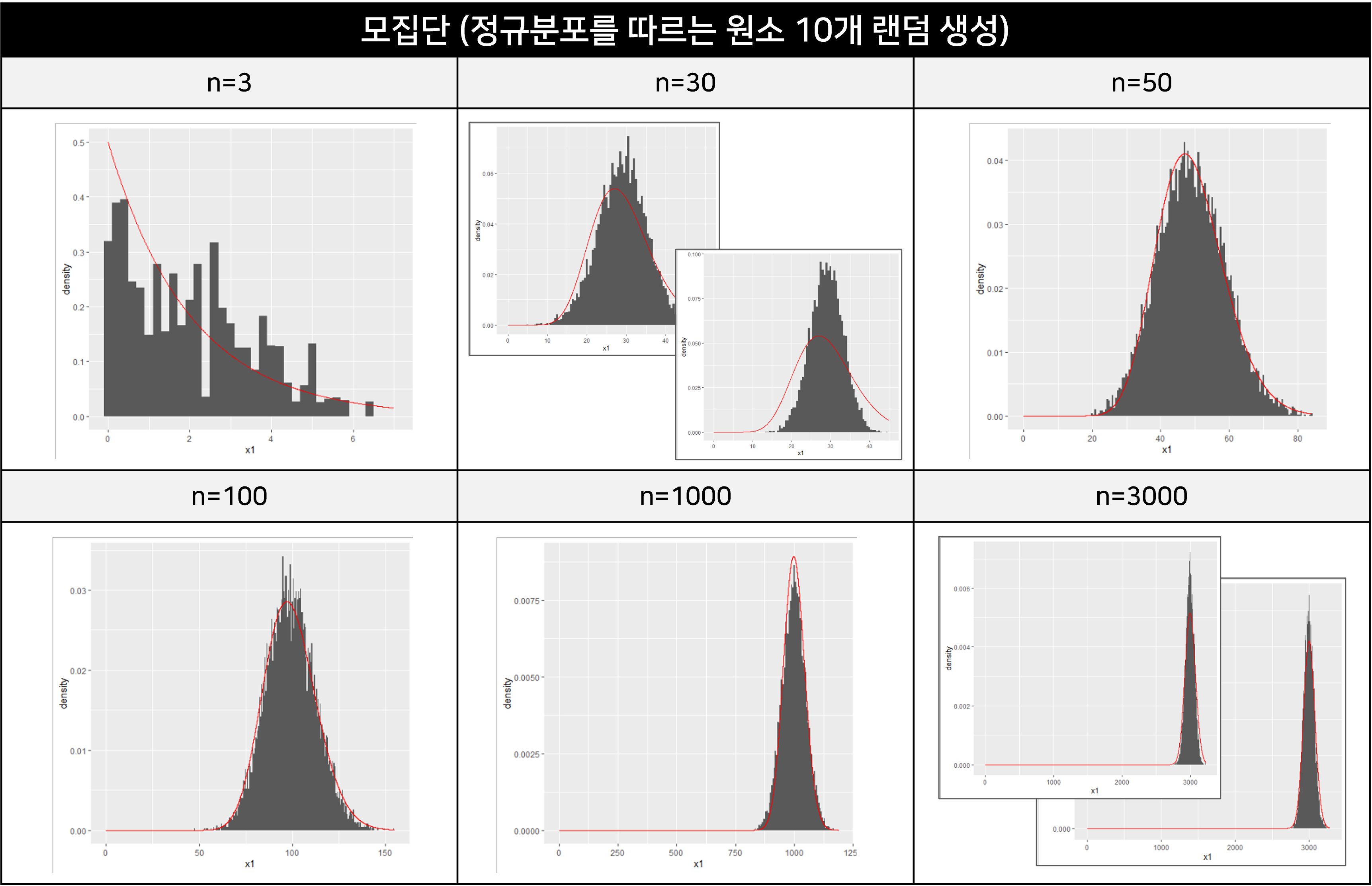
4-3) 모집단3 (표준정규분포에서 추출한 10개의 값)
표준정규분포에서 값 10개를 추출하여 모집단으로 삼았습니다. 모집단 1,2와 비교하면, 카이제곱분포와 훨씬 잘 일치합니다. 모집단 크기가 워낙 작기 때문에 어떤 값 10개가 결정되냐에 따라 일치도가 많이 달라지긴 합니다. 아래 그림의 n=30 을 보시면 모집단의 구성원소에 따라 일치도가 많이 달라짐을 보여줍니다.
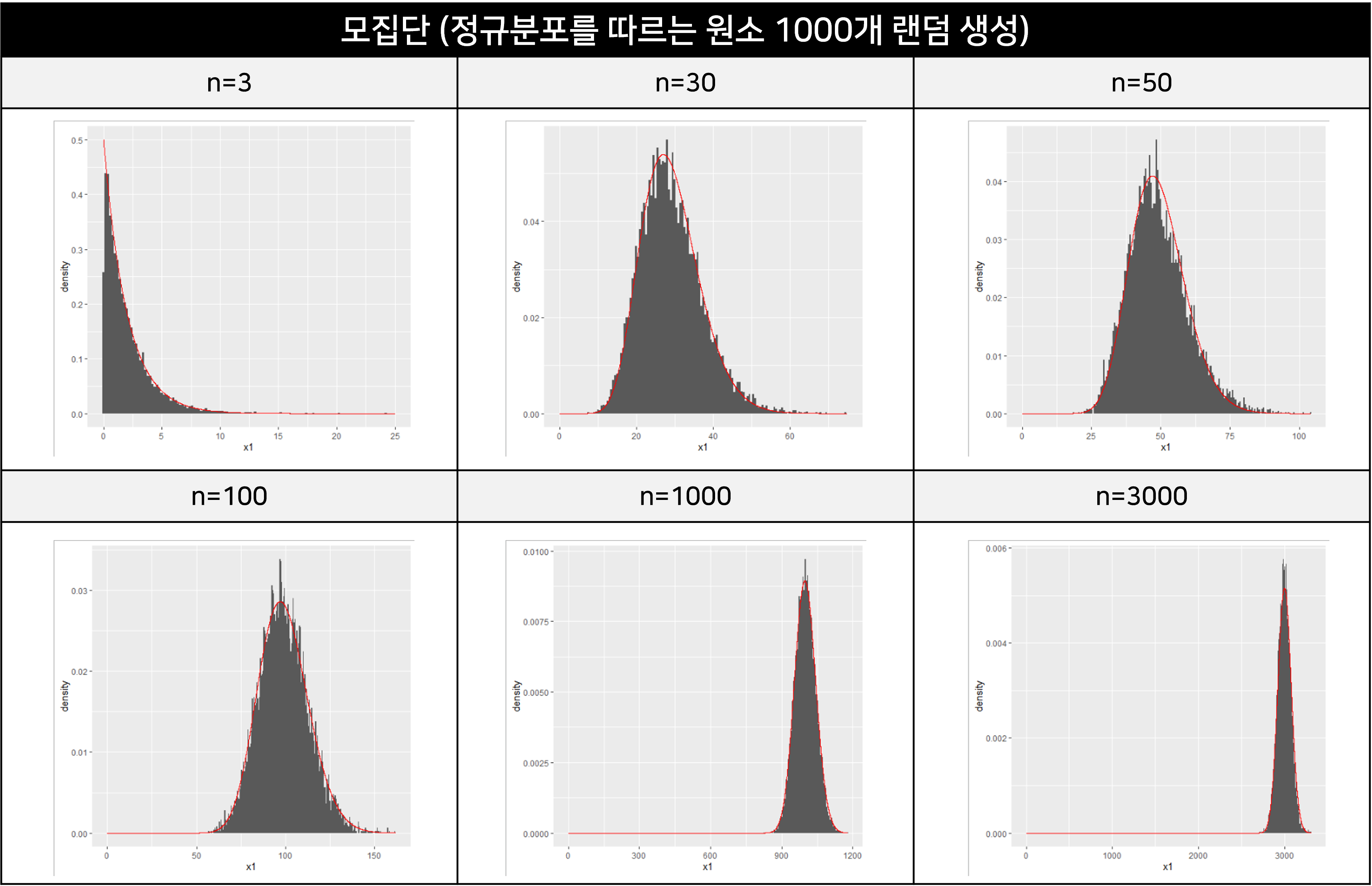
4-4) 모집단4 (표준정규분포에서 추출한 1000개의 값)
표준정규분포에서 값 1000개를 추출하여 모집단으로 삼았습니다. 정량적으로 확인을 해봐야겠지만 눈으로만 봤을때는 아주 잘 일치합니다.
5.고찰
균등분포를 따르는 단순한 모집단일 경우 표본이 아무리 커져도 카이제곱분포와 일치하지 않았습니다. 모양은 비슷하지만 값이 너무 달라서 표본분산의 분포를 카이제곱분포를 가정하고 사용하기 어려워 보입니다. 표본분산을 카이제곱분포로 가정하는 경우에는 반드시 모집단의 정규성이 확보되어야 할 것 같습니다. 표본이 커진다고 해결되지 않습니다.
이론상으로는 모집단과 상관 없이 표본만 커지면 카이제곱분포가 된다고 했는데, 왜 균등분포인 모집단에서는 성립하지 않는걸까요. 표본크기가 커지면 표본분산이 카이제곱분포를 따른다는 사실을 제대로 증명하지 않고 넘어간 것이 마음에 걸립니다. 제대로 증명해봐야 원인을 더 잘 찾을 수 있을 것 같습니다. 증명하기 전에 몇가지 비교를 더 하려고 합니다. 이어지는 강의는 아래와 같습니다.
90. 표본분산의 분포 시뮬레이션 (3) 누적분포함수 비교
91. 표본분산의 분포 시뮬레이션 (4) p값 비교
92. 표본분산의 분포에서 모집단 정규분포 조건제거 증명
'@ 필수과목 > 손으로 푸는 통계' 카테고리의 다른 글
| [손으로 푸는 통계 ver1.0] 93. 표본분산의 분포에서 모집단 정규분포 조건제거 증명 (2) 정규분포를 카이제곱분포로 근사 (0) | 2022.07.17 |
|---|---|
| [손으로 푸는 통계 ver1.0] 92. 표본분산의 분포에서 모집단 정규분포 조건제거 증명 (1) 의 분포 유도 (0) | 2022.07.16 |
| [손으로 푸는 통계 ver1.0] 91. 표본분산의 분포 시뮬레이션 (4) p값 비교 (0) | 2022.06.13 |
| [손으로 푸는 통계 ver1.0] 90. 표본분산의 분포 시뮬레이션 (3) 누적분포함수 비교 (0) | 2022.06.08 |
| [손으로 푸는 통계 ver1.0] 88. 표본분산의 분포 시뮬레이션 (1) 확률밀도함수 비교 (0) | 2022.05.12 |
| [손으로 푸는 통계 ver1.0] 87. 표본분산의 분포에서 모집단이 정규분포를 따라야 한다는 조건 제거하기 (0) | 2022.03.28 |
| [손으로 푸는 통계 ver1.0] 86. R로 카이제곱분포 그래프 그려보기 (0) | 2022.03.25 |
| [손으로 푸는 통계 ver1.0] 85. 카이제곱분포 형태 예측 (자유도 4자유도 이상 ) (0) | 2022.03.23 |




댓글
bigpicture님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.