비율검정과 카이제곱검정은 같은가 다른가

비율검정과 카이제곱검정을 두고 헷갈려 하시는 분들이 계실거라 생각됩니다. 뭔가 비슷한 것 같기도 한데 막상 구분해서 설명하자니 어려운 그런 혼란을 저도 겪었습니다. 오늘은 그 애매함을 해결해보도록 하겠습니다. 여기서 말하는 비율검정이란 일표본 비율검정과 이표본 비율검정을 말합니다.

 

일표본 비율검정 : 모비율과 표본 비율을 비교

이표본 비율검정 : 두 표본 비율을 비교

 

결론부터 말씀드리면 일표본 비율검정은 카이제곱 2수준 적합도검정과 같습니다. 이표본 비율검정은 2x2 분할표에서의 동질성검정과 같습니다. 

 

왜 그런지 하나씩 알아봅시다. 

 

1. 일표본 비율검정과 카이제곱 2수준 적합도검정

1-1) 일표본 비율검정

일표본 비율검정의 예시 하나를 가져옵시다. 

 

한국 남성의 흡연율이 60%라고 알려져 있다. 이를 확인하기 위해 한국남성 100명을 뽑았고 이들 중 흡연자는 70명이었다. 한국 남성의 흡연율이 60%가 아니라고 말할 수 있는가?

 

모비율과 표본비율은 아래와 같습니다.

 

모비율 : 60%
표본비율 : 70%

 

일표본 비율검정의 검정통계량은 아래와 같습니다. 

 

$z=\frac{ \hat{p}-p_{o} }{  \sqrt{ \frac{ p_{o} (1-p_{o}) }{n}  } }$

 

$\hat{p}$ : 표본 흡연자 비율

$p_{o}$: 모집단 흡연자 비율

$n$ : 표본 크기

 

검정통계량을 계산해봅시다. 

 

$z=\frac{ 0.7-0.6 }{  \sqrt{ \frac{ 0.6 (1-0.6) }{100}  } }=2.04$

 

p값을 계산하면 아래와 같습니다. 양측검정으로 계산하였습니다. 

 

> z=(0.7-0.6)/sqrt(0.6*(1-0.6)/100)
> (1-pnorm(z))*2
[1] 0.04122683

 

1-2) 카이제곱 2수준 적합도검정

위 예제를 분할표로 표현해봅시다.

 

	흡연	비흡연	합계
관찰	70	30	100
기대	60	40	100

 

카이제곱 검정을 이용하여 p값을 계산합시다. (correct를 FALSE로 해야 정규분포로 근사합니다.)

 

> prop.test(x=70,n=100,p=0.6,correct=FALSE)

	1-sample proportions test without continuity correction

data:  70 out of 100, null probability 0.6
X-squared = 4.1667, df = 1, p-value = 0.04123
alternative hypothesis: true p is not equal to 0.6
95 percent confidence interval:
 0.6041515 0.7810511
sample estimates:
  p 
0.7 

 

일표본 비율검정과 카이제곱 적합도 검정의 p값이 0.041로 동일합니다. 

 

 

2. 이표본 비율검정과 2x2 동질성검정

2-1) 이표본 비율검정

이표본 비율검정의 예시 하나를 가져옵시다. 남자와 여자의 흡연율 차이가 있는지 알고 싶어서 남자 100명과 여자100명을 대상으로 흡연율을 조사하였습니다. 남자의 흡연자는 50명이었고, 여자 흡연자는 30명이었습니다. 

 

두 표본비율은 아래와 같습니다.

 

남자 표본비율 : 50%
여자 표본비율 : 30%

 

이표본 비율검정의 검정통계량은 아래와 같습니다. 

 

$z=\frac{ \hat{p}_{1} - \hat{p}_{2}  }{
\sqrt{ 
\hat{p}(1-\hat{p})\left ( \frac{1}{n_{1}} + \frac{1}{n_{2}} \right )
}
}$

 

$\hat{p}=\frac{x_{1}+x_{2}}{n_{1}+n_{2}}$

 

$\hat{p}_{1}$ : 남자 흡연자 비율

$\hat{p}_{1}$: 여자 흡연자 비율

$x_{1}$ : 남자 흡연자 수

$x_{2}$ : 여자 흡연자 수

$n_{1}$ : 남자 표본 크기

$n_{2}$ : 여자 표본 크기

 

검정통계량을 계산해봅시다. 

 

$\hat{p}=\frac{50+30}{100+100}=0.4$

 

$z=\frac{ 0.5 - 0.3  }{
\sqrt{ 
0.4(1-0.4)\left ( \frac{1}{100} +\frac{1}{100}  \right )
}
}=2.886$

 

p값을 계산하면 아래와 같습니다. 양측검정으로 계산하였습니다.  (correct를 FALSE로 해야 정규분포로 근사합니다.)

 

> z=(0.5-0.3)/sqrt(0.4*(1-0.4)*(1/100+1/100))
> (1-pnorm(z))*2
[1] 0.003892417

 

2-2) 2x2 동질성검정

위 예제를 분할표로 표현해봅시다. 

 

	흡연	비흡연	합계
남성	50	50	100
여성	30	70	100
합계	80	120	200

 

카이제곱 검정을 이용하여 p값을 계산합시다. 

 

> prop.test(x=c(50,30),n=c(100,100),correct=FALSE)

	2-sample test for equality of proportions without continuity correction

data:  c(50, 30) out of c(100, 100)
X-squared = 8.3333, df = 1, p-value = 0.003892
alternative hypothesis: two.sided
95 percent confidence interval:
 0.06706878 0.33293122
sample estimates:
prop 1 prop 2 
   0.5    0.3 

 

이표본 비율검정과 2x2 동질성검정의 p값이 0.003892로 동일합니다. 

 

 

3. 결론

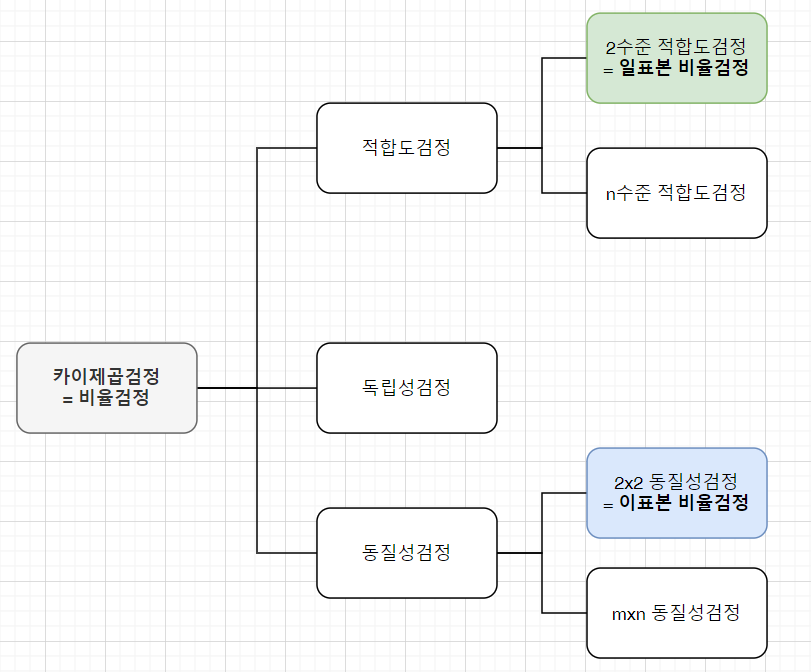
일표본 비율검정은 카이제곱검정의 2수준 적합도검정과 같고, 이표본 비율검정은 카이제곱검정의 2x2 동질성검정과 같습니다. 카이제곱 검정은 더 많은 수준에서도 수행이 가능하기 때문에 카이제곱검정이 일표본 비율검정과 이표본 비율검정을 포함한다고 할 수 있습니다. 카이제곱 자체를 비율검정이라고 부르기도 합니다. 정리하면 아래와 같습니다.