t분포 글 하나로 끝내버리기

1. 어디에 사용되나요?

t분표는 t검정에 사용됩니다. t검정이 분산분석의 사후분석, 상관분석, 회귀분석 과정에도 사용되기 때문에 t분포가 이러한 검정에서 사용된다고 할 수 있습니다. 

 

2. 어떻게 생겼나요? 

t분포 함수의 수식은 아래와 같습니다. 

 

$f(t)=\frac{\Gamma\left ( \frac{\nu+1}{2} \right )}{\sqrt{\nu \pi}\ \Gamma\left ( \frac{\nu}{2} \right )}
\left ( 1+\frac{t^2}{\nu} \right )^{-\left ( \frac{\nu+1}{2} \right )}$

 

t분포의 모양을 결정하는 파라미터는 $\nu$ 하나밖에 없습니다. $\nu$는 자유도입니다. 표본 크기가 n 인 경우 자유도 $\nu$는 n-1입니다. 

 

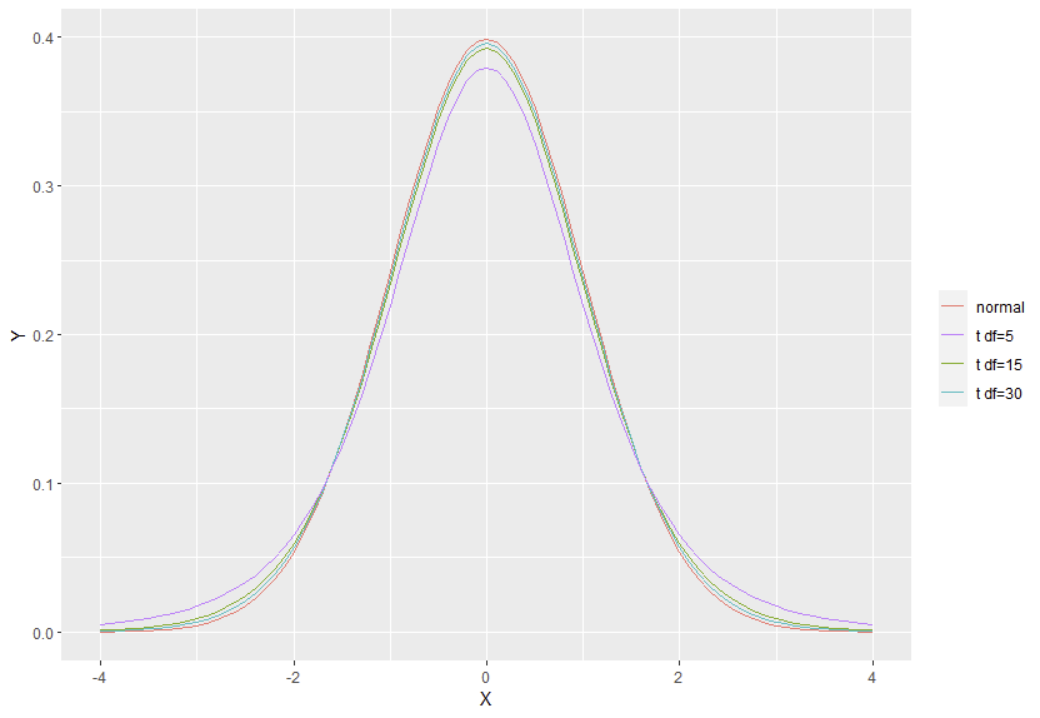
여러 자유도의 t분포를 그래프로 그려보면 아래와 같습니다. 

 

 

3. 어떤 의미를 갖나요? 

t분포는 t라는 확률변수의 분포입니다. t라는 확률 변수의 확률밀도가 어떻게 분포하고 있는지 알려주는 함수입니다. t분포를 이해하려면 t가 무엇인지 알아야 합니다. t는 아래와 같이 정의 됩니다. 

 

$t=\frac{\bar{X}-\mu}{\frac{s}{\sqrt{n}}}$

 

먼저 위 식을 있는 그대로 설명해보겠습니다. $\bar{X}$는 표본평균입니다. $\mu$는 모평균입니다. 따라서 t값의 분자인 $\bar{X}-\mu$는 표푠평균과 모평균의 차이입니다. 분모의 s는 표본분산이고 n은 표본의 크기입니다. t값이 무엇인지 이해가 되시나요? t값을 구성하고 있는 각 인수들에 대한 설명을 들어도 t값이 무엇을 의미하는지 아마 이해가 안되실겁니다. 변수 t를 이해하려면 t가 등장한 맥락을 알아야 합니다. 긴 이야기가 될 것이라 관심 없으신 분들은 3번으로 바로 넘어가시면 됩니다. 

 

중심극한정리부터 이야기를 시작하겠습니다. 모집단에서 표본을 뽑는 상황을 가정해봅시다. 중심극한정리는 모집단에서 뽑는 표본의 크기가 충분히 크다면, 모집단의 분포에 상관 없이 표본평균의 분포가 정규분포를 따른다는 정리입니다. 표본평균의 평균은 모평균이고, 표본평균의 분산은 모분산을 n으로 나눈 것과 같으므로 표본평균의 분포는 아래와 같은 정규분포를 따릅니다.

 

$\bar{X}\sim N\left ( \mu,\frac{\sigma^2}{n} \right )$

 

위 식에서 $\mu$는 모평균, $\sigma^2$은 모분산, n은 표본의 크기입니다. 정규 분포 형태로 다루는 것 보다 표준정규분포 형태로 다루는 것이 더 편하기 때문에 표준화시키겠습니다. 

 

$\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\sim N\left ( 0,1 \right )$

 

위 식의 좌변을 확률변수 Z라고 놓겠습니다. Z는 표준정규분포를 따르는 확률변수입니다. 

 

$Z=\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}$

 

Z값을 이용하는 통계검정을 Z검정이라고 부릅니다. Z값에는 한가지 한계가 있었는데요. 모분산인 $\sigma$를 모른다는 것이었습니다. 모평균도 몰라서 검정을 하고 있는데 모분산을 알수 있을리가 없습니다. 어쩔 수 없이 Z검정에서는 추출한 표본에서 계산된 표본분산을  모분산 대신 사용해왔습니다. 이런 문제를 해결하고자 t분포가 고안되었습니다. t분포는 표본평균과 표본표준편차를 둘 다 확률변수로 고려 하여 유도된 분포입니다. 유도과정을 아주 간단히만 살펴봅시다. 확률변수인 t 는 아래와 같습니다. 

 

$t=\frac{\bar{X}-\mu}{\frac{s}{\sqrt{n}}}$

 

위 식을 아래와 같이 변형할 수 있습니다. 

 

$t=\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}} }\frac{1}{\sqrt{\frac{ns^2}{\sigma^2}} }\sqrt{n}$

 

모집단이 정규분포를 따른다고 가정하면 우변의 첫째항은 표준정규분포를 따릅니다. 두번째 항 루트 안의 확률변수는 n자유도 카이제곱분포를 따릅니다. 표준정규분포를 따르는 확률변수를 Z, n자유도 카이제곱분포를 따르는 확률변수를 V라고 놓으면 아래와 같습니다. 

 

$t=Z\frac{1}{\sqrt{V} }\sqrt{n}$

 

표준정규분포와 카이제곱분포를 이용하여 위 식 우변의 분포를 유도하면 t분포가 유도됩니다. t분포는 모집단이 정규분포를 따른다고 가정하고 유도된 분포라는 것을 기억합시다. t분포를 사용하려면 모집단의 정규성이 확보되어야 합니다. 

 

t분포는 모분산을 단순히 표본분산으로 대체하여 Z분포를 이용하는 것이 아니라, 표본 분산 자체가 변수인 새로운 분포를 유도한 것입니다. 

 

4. 어떤 성질이 있나요? 

1) 평균은 0이고, 표준편차는 $\sqrt{\frac{\nu}{\nu-2}}$ 입니다. 자유도인 $\nu$ 가 커지면 표준편차는 1에 가까워갑니다. 

 

2) 표준정규분포인 Z 분포 보다 꼬리가 두껍습니다. 아래 그래프를 보면 t분포인 파란색 그래프의 꼬리가 Z분포인 빨간색 그래프의 꼬리 보다 두껍습니다. 아래 그림의 t분포는 자유도가 5인 경우입니다. 

 

3) t분포는 자유도가 커지면 정규분포에 가까워져 갑니다. 아래 그래프는 자유도 5,15,30인 t분포입니다. 자유도가 커질 수록 정규분포(빨간색)에 가까워져 가는 것을 알 수 있습니다.