지난 시간에 우리는 가우스가 정규분포를 유도한 과정을 살펴봤습니다. 직접 유도하는 것은 기초강의의 수준을 넘어가기 때문에 과정만 간단히 알아보았습니다. 가우스가 유도한 정규분포의 수식은 아래와 같습니다.
$$
f(x)=\frac{1}{\sqrt{2\pi }\sigma}e^{-\frac{(x-m) ^2}{2\sigma^2}}
$$
오늘은 이 수식의 그래프를 그려보겠습니다. 수식의 의미는 다음시간에 자세히 다뤄보도록 할게요. 처음부터 위 함수를 그리기는 너무 어렵습니다. 가장 단순한 형태부터 출발합시다. 가장 단순한 형태는 아래와 같습니다.
$$
f(x)=e^{-x^2}
$$
이 함수는 자연상수 e를 밑으로 하는 지수함수입니다. e는 약 2.7정도의 값을 갖는 무리수입니다. 위 함수의 형태를 대략적으로 예상해봅시다. x가 0일때의 함수값은 1입니다. x가 0보다 커지면 e의 지수부분이 음의 무한대가 되므로 함수 값은 0에 가까워집니다. x가 0보다 작아져도 e의 지수부분이 음의 무한대가 되므로 함수 값이 0에 가까워집니다. 따라서 이 함수는 0을 중심으로 좌우 대칭이고 가운데가 볼록한 형태의 함수입니다. 그려보면 아래와 같습니다.
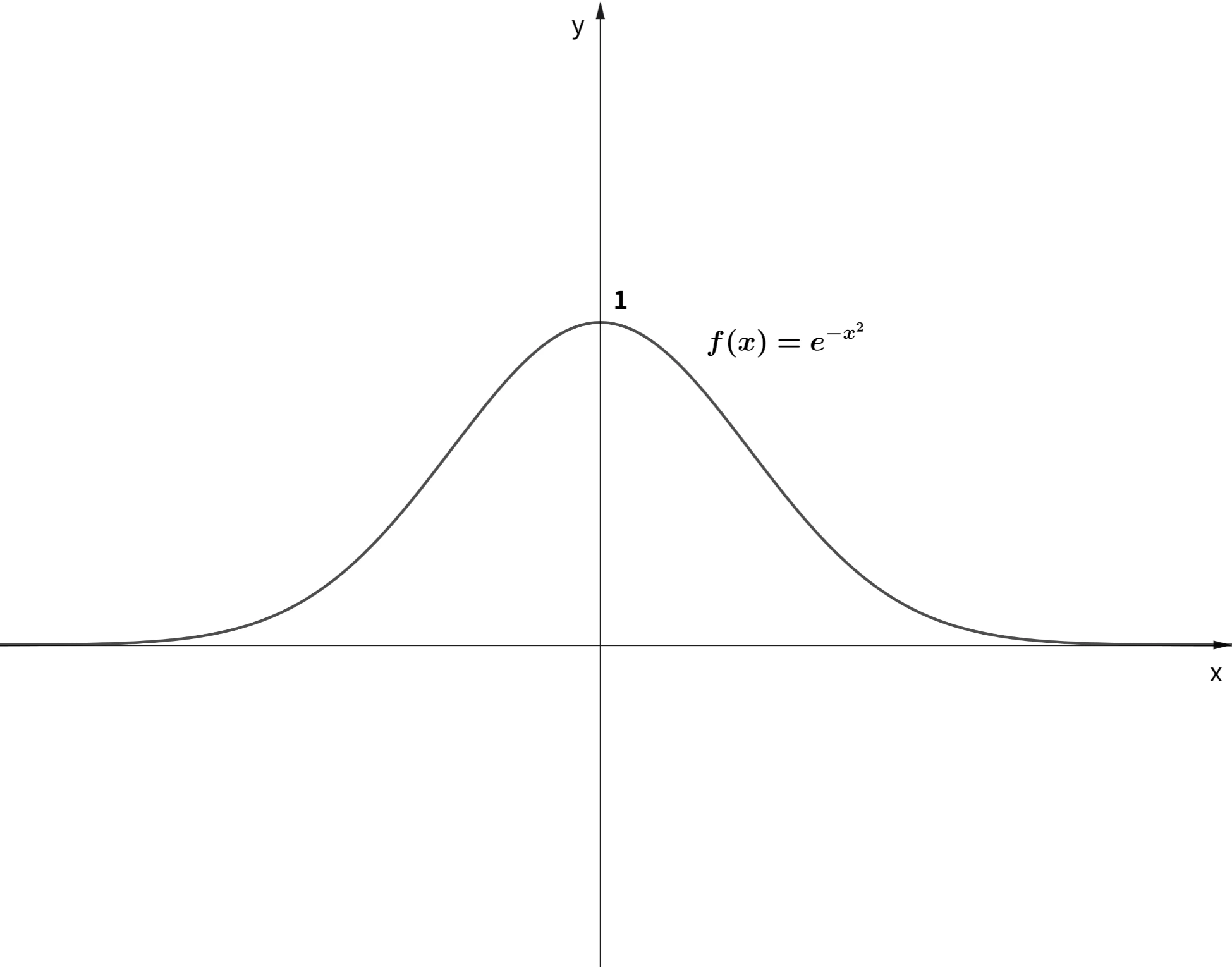
종을 뒤집어놓은 모양과 닮았습니다. 이번에는 위 함수를 x축으로 m 만큼 이동해봅시다. 함수의 수식은 아래와 같습니다.
$$
f(x)=e^{-(x-m)^2}
$$
그래프로 그려보면 아래와 같습니다.
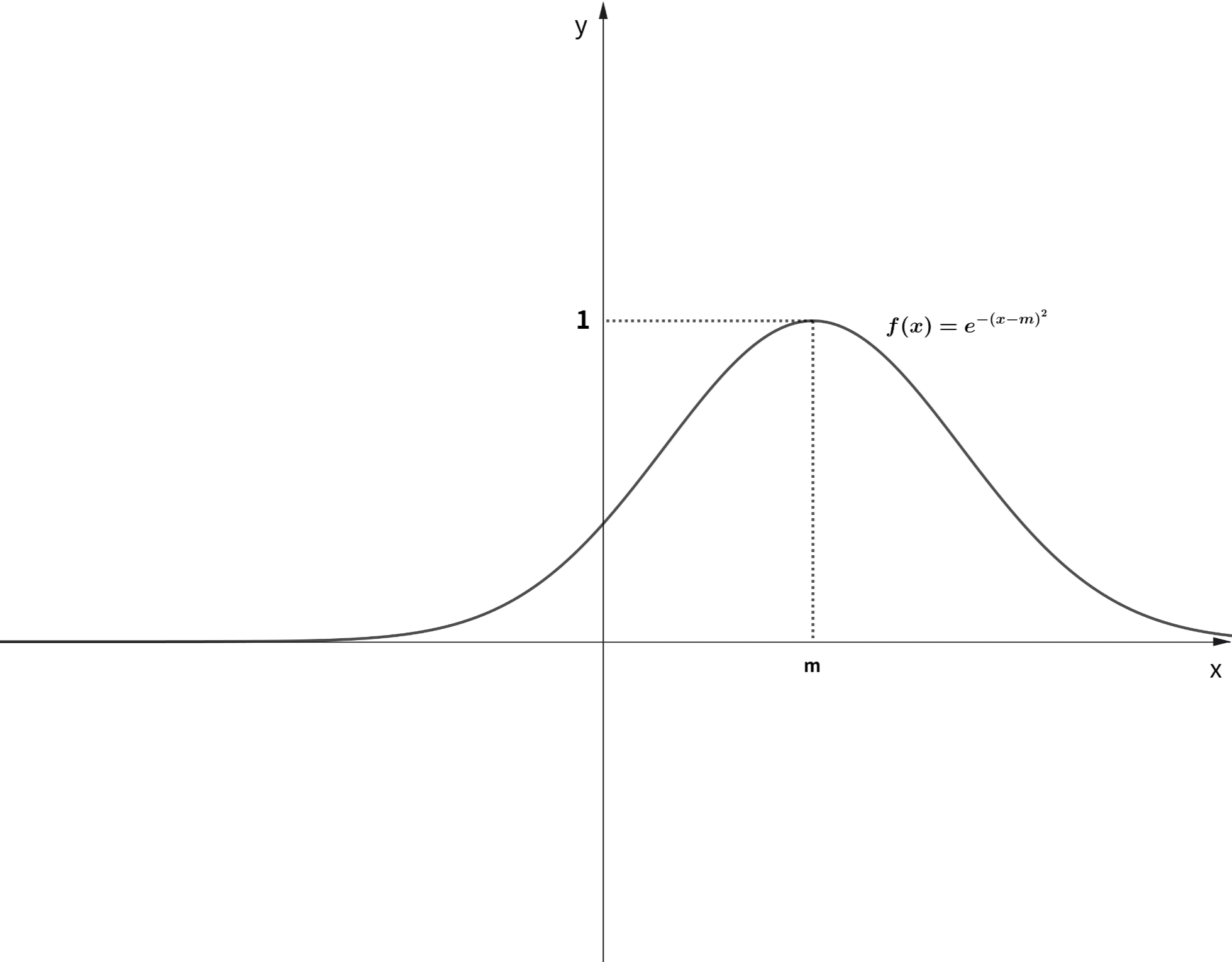
m을 중심으로 좌우 대칭인 그래프입니다. 이번에는 아래와 같이 계수를 추가해봅시다.
$$
f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-(x-m)^2}
$$
앞에 곱해진 계수가 양수이므로 전체적인 모양은 동일합니다. 달라진 것이 있다면 가장 볼록한 함수값입니다. 가장 볼록한 부분의 함수값이 1이 아니라 $frac{1}{\sqrt{2\pi}\sigma}$입니다. 그래프는 아래와 같습니다.
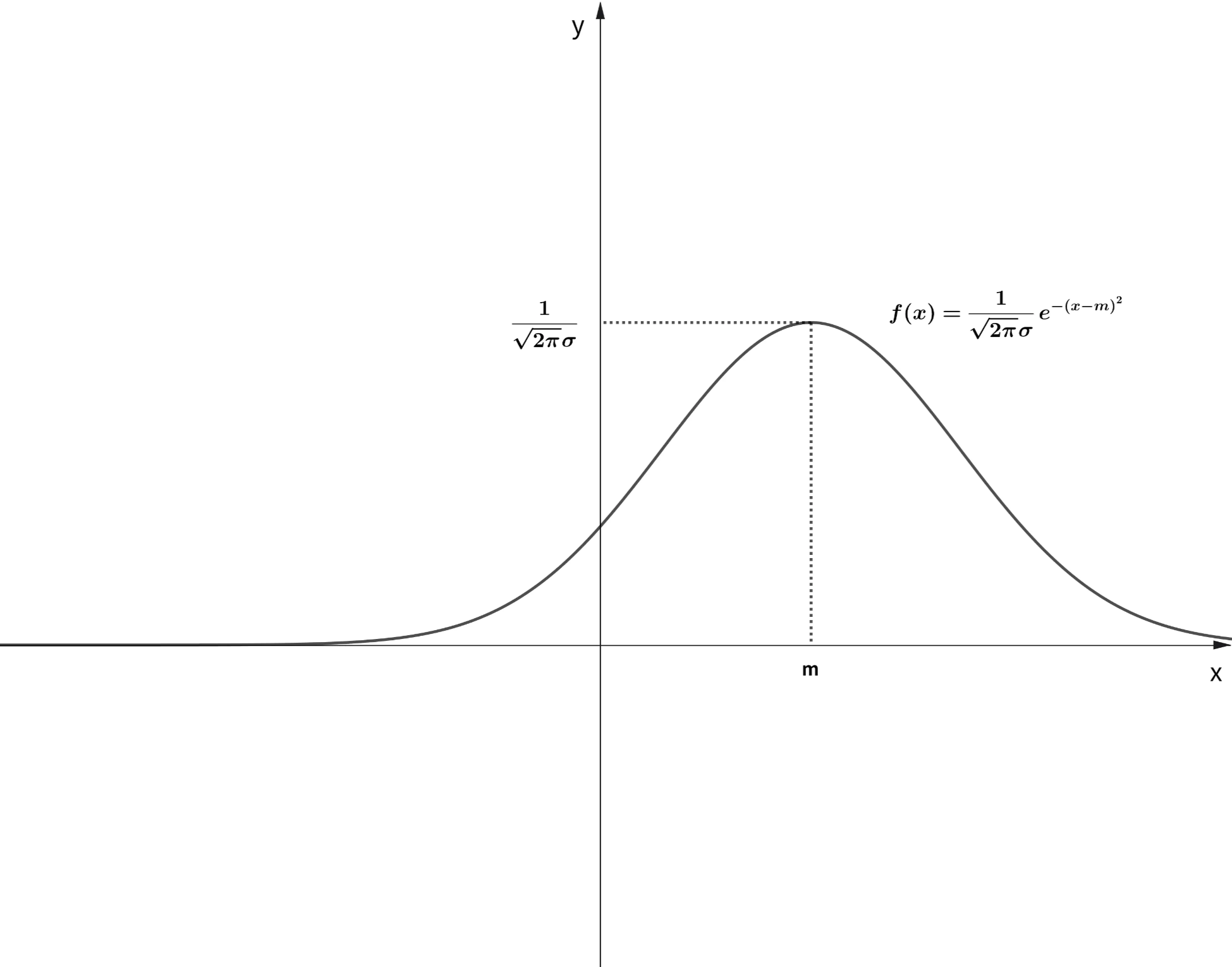
이제 한단계만 더 바꾸면 정규분포 그래프가 됩니다. 아래와 같습니다.
$$
f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-m)^2}{2\sigma^2}}
$$
m 을 중심으로 대칭은 종모양의 그래프입니다. x가 m일때 가장 큰 함수값을 갖고, 함수값은 $\frac{1}{\sqrt{2\pi}\sigma}$ 입니다. 그래프는 아래와 같습니다.

위 식에서 $\sigma$가 커지면 그래프가 어떻게 바뀔까요? 우변의 첫번째 항인 $\frac{1}{\sqrt{2\pi}\sigma}$는 작아지는 반면, 두번째 항은 커집니다. $\sigma$가 분모에 있기 때문입니다. 전체 값은 어떻게 될까요? 최댓값인 ${\sqrt{2\pi}\sigma}$은 작아지므로 가장 높은 값 주변부는 아래쪽으로 내려오게 됩니다. 하지만 여기서 기억해야할 사실이 하나 있습니다. 확률밀도함수의 적분값은 항상 1이라는 것입니다. 그래프와 x축 사이의 넓이가 1이라는 말입니다. 따라 가장 볼록한 부분이 아래로 내려오면 끝부분으로 갈 수록 값이 커집니다. 그림으로 나타내면 아래와 같습니다. 빨간색 그래프가 $\sigma$가 커진 그래프입니다.

오늘은 정규분포의 그래프를 그려보았습니다. 우리는 아래와 같은 세가지 내용을 배웠습니다.
1. 정규분포의 그래프는 종을 엎어놓은 모양이다.
2. 정규분포의 그래프는 m을 중심으로 대칭이다.
3. 정규분포의 그래프에서 $\sigma$가 커지면 가장 높은 봉우리는 낮아지고, 양 끝부분은 함수 값이 커집니다.
다음 시간에는 정규분포의 수식을 자세히 이해해봅시다.
'기초과목 > 확률과통계 기초' 카테고리의 다른 글
| [확률과 통계 기초] 3-46. 정규분포의 발견 (3) 오차의 분포로 부터 (0) | 2025.12.26 |
|---|---|
| [확률과 통계 기초] 3-45. 정규분포의 발견 (2) 이항분포로 부터 (0) | 2025.11.22 |
| [확률과 통계 기초] 3-44. 정규분포의 발견 (1) 프롤로그 (0) | 2025.11.17 |
| [확률과 통계 기초] 3-43. 가능성이 변하는 연속확률변수의 확률함수 (0) | 2025.10.16 |
| [확률과 통계 기초] 3-42. 균등분포의 평균, 분산, 표준편차 (0) | 2025.10.07 |
| [확률과 통계 기초] 3-41. 연속확률 분포 적분구간을 무한대로 해도 되는 이유 (0) | 2025.09.04 |
| [확률과 통계 기초] 3-40. 구간 표현 익히기 [a,b] (a,b) (0) | 2025.08.30 |
| [확률과 통계 기초] 3-39. 연속확률분포의 분산과 표준편차 (0) | 2025.07.31 |
댓글