1738년, 드무아브르는 n이 무한히 커지면, p=1/2 일때 이항분포가 종 모양의 곡선에 가까워져 간다는 것을 증명했습니다. 이 종 모양의 곡선이 표준정규분포입니다. 1812년 라플라스는 p를 0과 1 사이로 일반화시켰습니다.
동전던지기 예시를 가지고 이항분포에서 n이 커질 때, 종 모양의 곡선이 되는지 시험해봅시다.
동전던지기 예시의 이항분포 함수는 아래와 같습니다.
$$
p(x)=_nC_x \left( \frac{1}{2} \right)^{x}\left( \frac{1}{2} \right)^{n-x}
$$
동전을 세번 던질때 확률분포를 그래프로 그려봅시다. 동전을 세번 던질 때 이항분포 함수는 아래와 같습니다.
$$
p(x)=_3C_x \left( \frac{1}{2} \right)^{x}\left( \frac{1}{2} \right)^{3-x}
$$
함수 값을 구해보면 아래와 같습니다.
| X | 0 | 1 | 2 | 3 |
| P(X) | \frac{1}{8} | \frac{3}{8} | \frac{3}{8} | \frac{1}{8} |
그래프로 그려보면 아래와 같습니다.
동전을 10, 30, 50, 100번 던질 때의 그래프는 R 을 이용해서 그렸습니다. 아래와 같습니다.
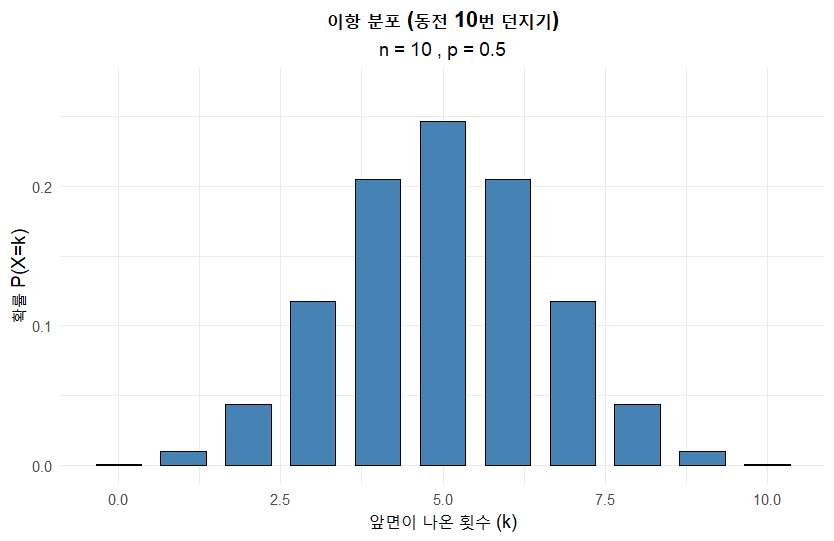
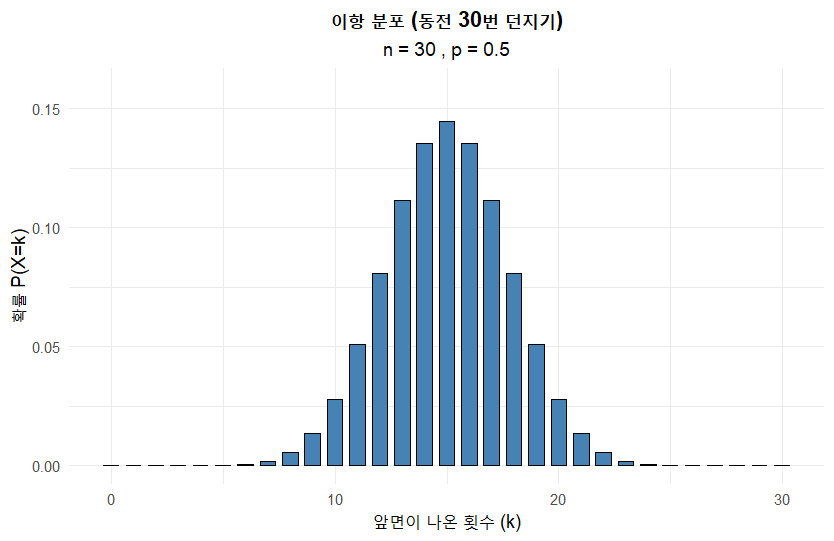
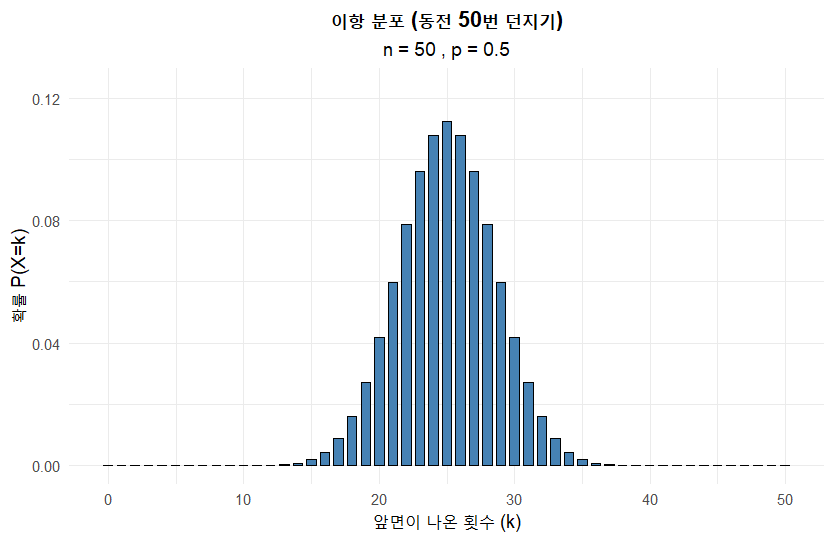
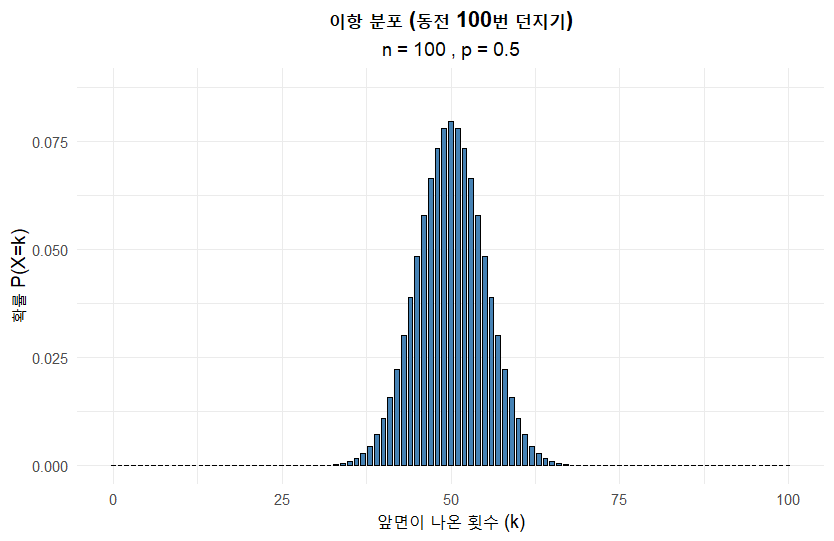
모양이 좌우 대칭인 종 모양에 가까워지는 것을 확인할 수 있습니다. 동전이 0.5니까 당연히 대칭으로 나오는게 아니냐는 의문이 들 수도 있어서, 대칭이 아닌 경우를 가정하고 그려보았습니다. 앞면이 나올 확률을 0.2로 놓고 그래프를 그려보면 아래와 같습니다.
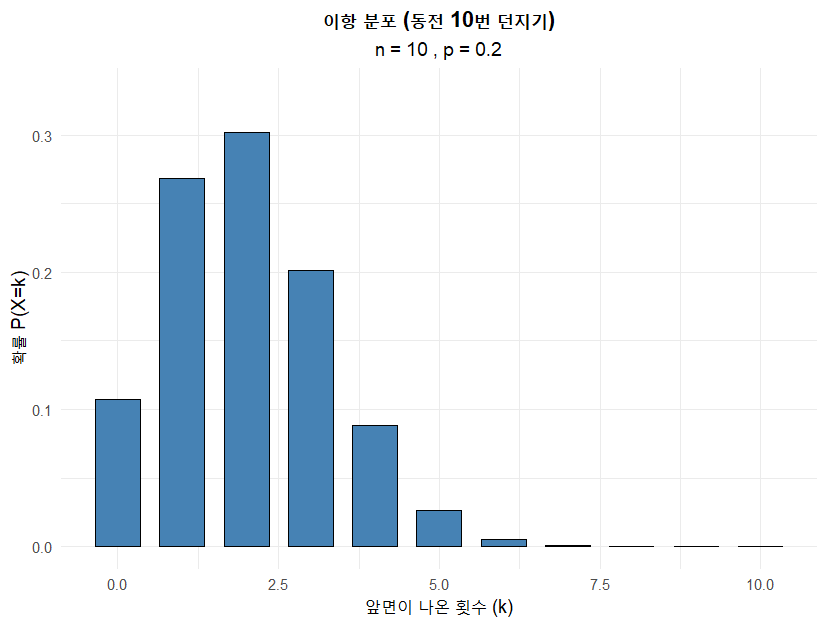
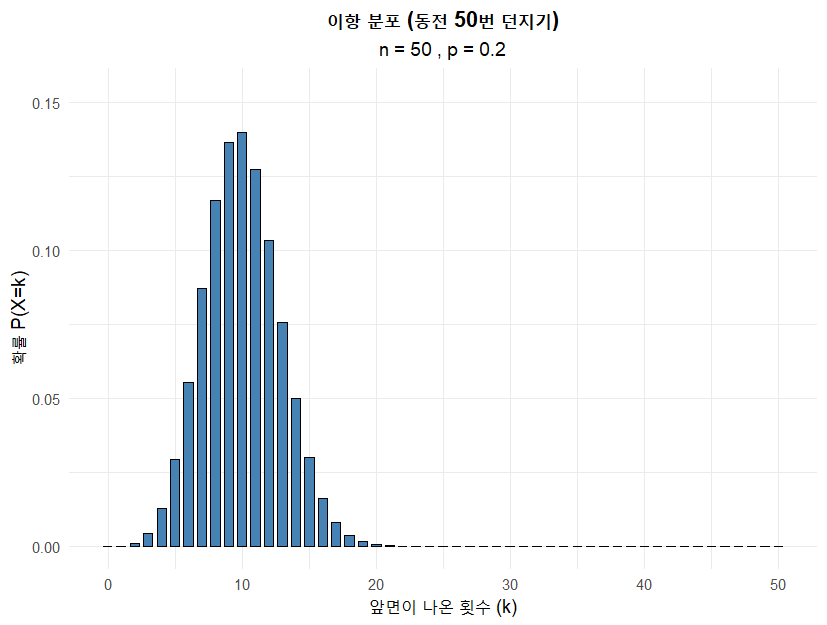
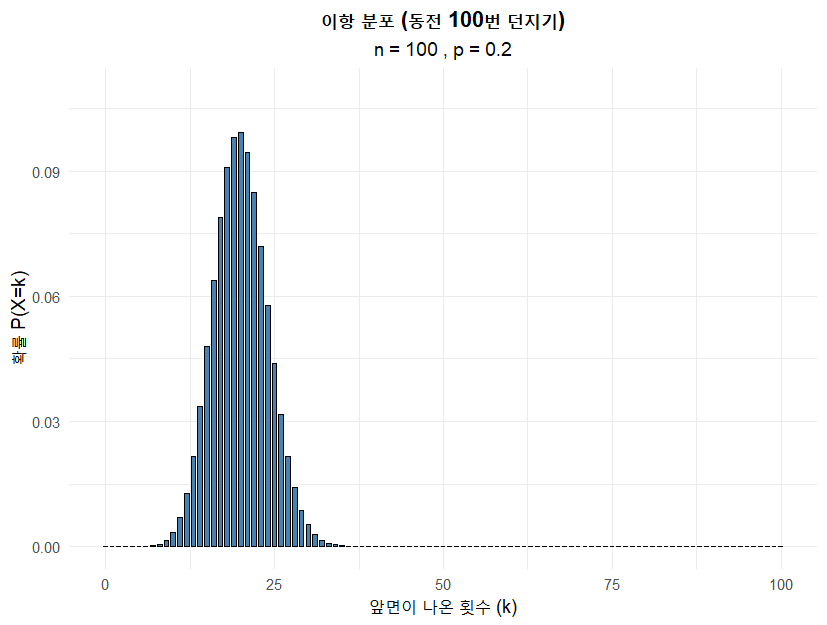
동일하게 n이 커질 수록 종 모양이 됩니다. 같은 위치에서 종모양으로 변하는건 아니고 그래프가 전체적으로 오른쪽으로 이동합니다. 그래프 x 축 범위가 변하고 있음에 주목해 주세요.
표준정규분포가 무엇인지 모르는 상태이므로 아래 사실만 받아들이고 넘어갑시다.
“이항분포에서 n이 무한이 커지면 표준 정규분포가 된다.”
정규분포와 표준정규분포를 배운 뒤에 이항분포가 표준정규분포에 수렴하는 것에 대해 한번 더 다루겠습니다.
#강의 영상
https://www.youtube.com/watch?v=fOnSl2htYZo
'기초과목 > 확률과통계 기초' 카테고리의 다른 글
| [확률과 통계 기초] 3-47. 정규분포의 그래프 (0) | 2026.01.24 |
|---|---|
| [확률과 통계 기초] 3-46. 정규분포의 발견 (3) 오차의 분포로 부터 (0) | 2025.12.26 |
| [확률과 통계 기초] 3-44. 정규분포의 발견 (1) 프롤로그 (0) | 2025.11.17 |
| [확률과 통계 기초] 3-43. 가능성이 변하는 연속확률변수의 확률함수 (0) | 2025.10.16 |
| [확률과 통계 기초] 3-42. 균등분포의 평균, 분산, 표준편차 (0) | 2025.10.07 |
| [확률과 통계 기초] 3-41. 연속확률 분포 적분구간을 무한대로 해도 되는 이유 (0) | 2025.09.04 |
| [확률과 통계 기초] 3-40. 구간 표현 익히기 [a,b] (a,b) (0) | 2025.08.30 |
| [확률과 통계 기초] 3-39. 연속확률분포의 분산과 표준편차 (0) | 2025.07.31 |
댓글