이전 글에서 ‘가능성이 변하는 연속확률변수’에 대해 이야기한 적이 있습니다. 몸무게가 변하는 약 예시였는데요. 먹으면 몸무게가 60~100kg 으로 랜덤하게 변하는 약이 있을 때, 60kg으로 변할 가능성이 가장 작고 100kg에 가까워질 수록 가능성이 커진다고 가정했습니다. 약을 먹고 변한 몸무게를 확률변수 X라고 놓았을 때, X의 확률함수는 무엇인가? 라는 의문이 있었지만 해결하지 못했었습니다.
이제 우리는 확률밀도함수가 무엇인지 배웠으니, 위 예시를 수식으로 표현할 수 있습니다. 먼저 확률밀도함수를 아래와 같이 그릴 수 있습니다. 가능성은 직선형태로 증가한다고 가정하겠습니다.
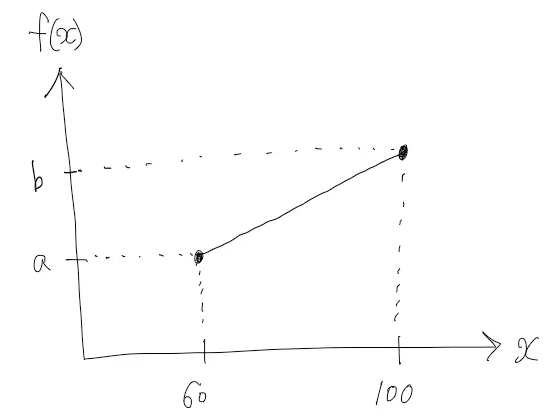
이제 a와 b를 구해야 합니다. 전체 확률이 1이 되어야 하므로 아래 그림의 넓이 S가 1이어야 합니다.
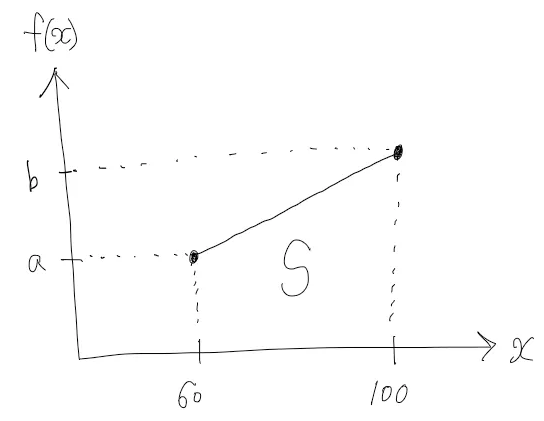
아래 그림처럼 사각형에서 삼각형 넓이를 빼는 방법으로 S를 구하겠습니다.
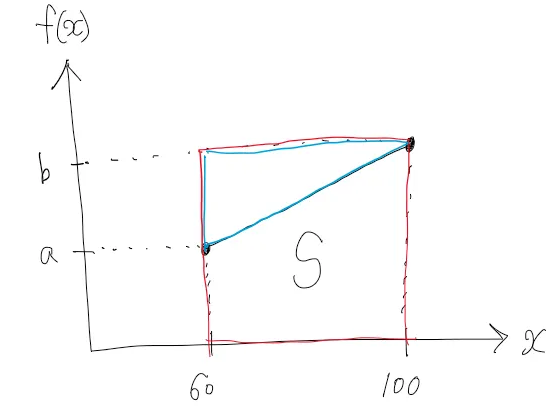
$$S=b\times 40 -\frac{1}{2}(b-a)\times 40=1$$
계산하면 아래와 같습니다.
$$
S=20(a+b)=1
$$
위 식만 가지고는 a와 b 를 정할 수 없습니다. 조건을 하나 추가해주겠습니다. 100kg 이 될 확률이 60kg 이 될 확률의 2배이다(b=2a)라는 조건을 추가해줍시다. 위 식의 b에 2a를 넣어주면 아래와 같습니다
$$
S=20(a+2a)=1
$$
a는 아래와 같이 계산됩니다.
$$
a=\frac{1}{60}
$$
그래프로 나타내면 아래와 같습니다.
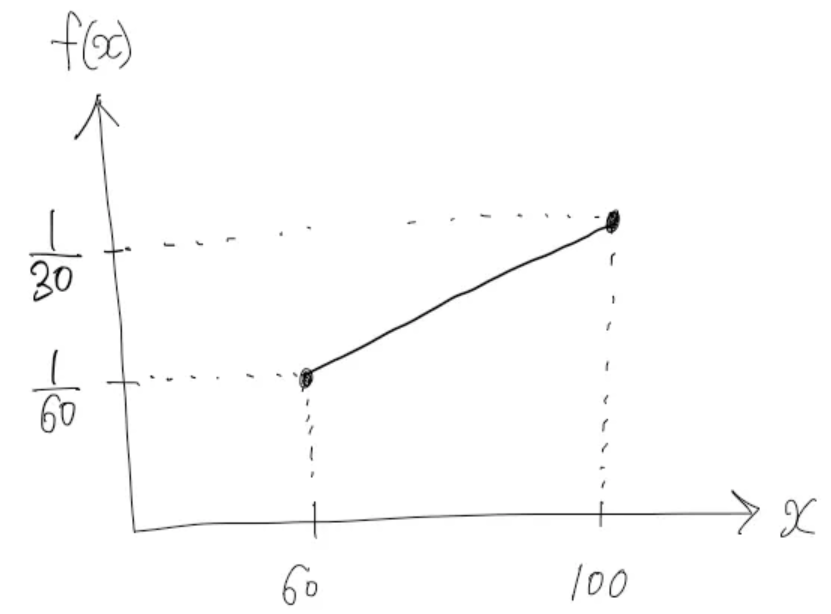
오늘은 아래 조건을 만족하는 확률변수의 확률밀도함수를 구해보았습니다.
- 먹으면 몸무게가 60~100kg 으로 랜덤하게 변하는 약이 있을 때, 변한 몸무게를 확률밀도함수 X라고 놓음
- 60kg으로 변할 가능성이 가장 작고 100kg에 가까워질 수록 가능성이 커짐
- 100kg 이 될 확률밀도가 60kg 의 두배
https://www.youtube.com/watch?v=crHNwk0FJgA
'기초과목 > 확률과통계 기초' 카테고리의 다른 글
| [확률과 통계 기초] 3-47. 정규분포의 그래프 (0) | 2026.01.24 |
|---|---|
| [확률과 통계 기초] 3-46. 정규분포의 발견 (3) 오차의 분포로 부터 (0) | 2025.12.26 |
| [확률과 통계 기초] 3-45. 정규분포의 발견 (2) 이항분포로 부터 (0) | 2025.11.22 |
| [확률과 통계 기초] 3-44. 정규분포의 발견 (1) 프롤로그 (0) | 2025.11.17 |
| [확률과 통계 기초] 3-42. 균등분포의 평균, 분산, 표준편차 (0) | 2025.10.07 |
| [확률과 통계 기초] 3-41. 연속확률 분포 적분구간을 무한대로 해도 되는 이유 (0) | 2025.09.04 |
| [확률과 통계 기초] 3-40. 구간 표현 익히기 [a,b] (a,b) (0) | 2025.08.30 |
| [확률과 통계 기초] 3-39. 연속확률분포의 분산과 표준편차 (0) | 2025.07.31 |
댓글