반응형
연속확률분포의 기댓값 수식을 살펴봅시다.
연속확률분포의 기댓값 : $\int_{a}^{b}xf(x)dx$
위 확률분포는 $[a,b]$에서 정의된 확률분포입니다. 그 외의 값은 0입니다. 그래프로 나타내보면 아래와 같습니다. 모양은 임의로 표현했습니다.
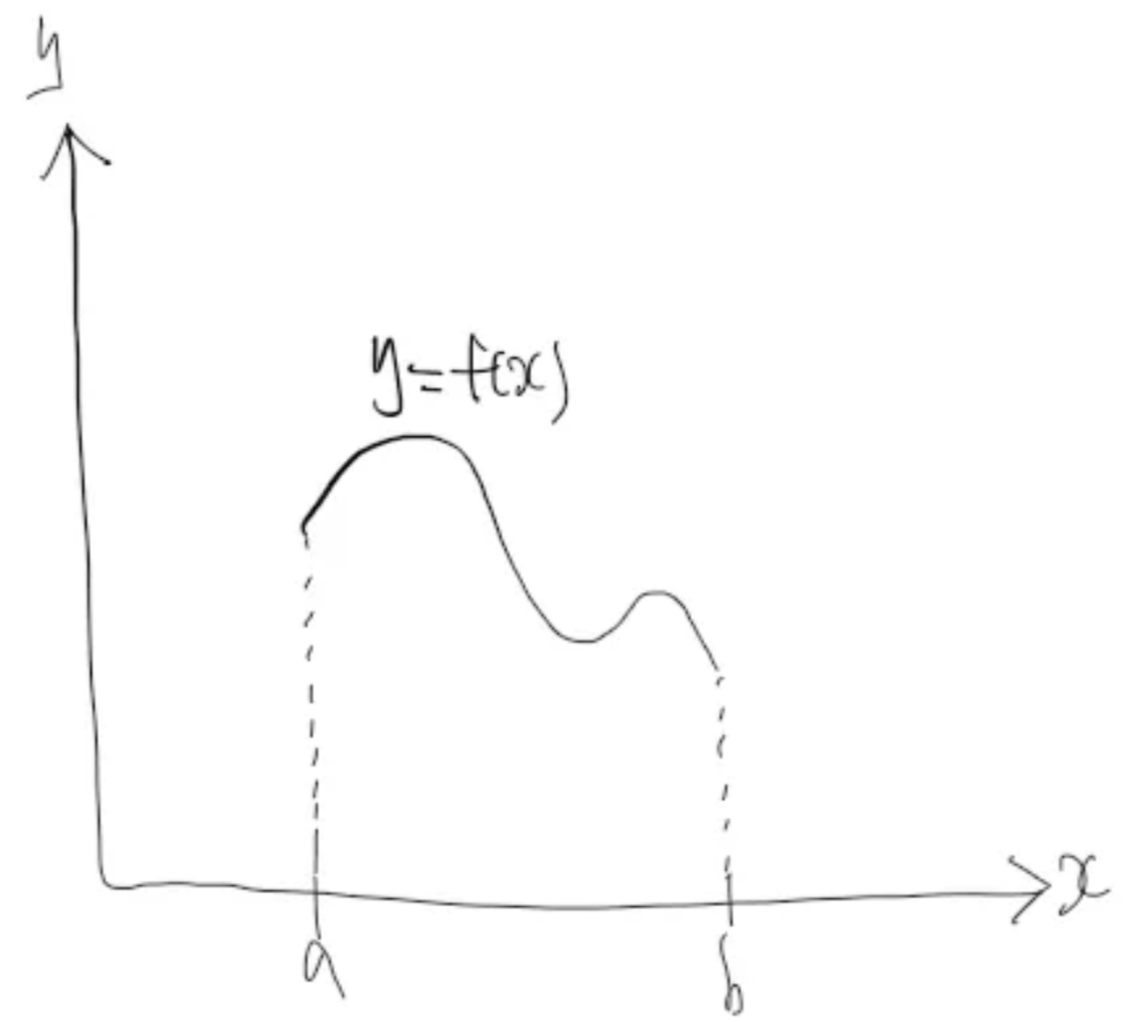
$[a,b]$ 이외 구간에서 $f(x)$의 값은 0입니다. 따라서 $-\infty$부터 $\infty$까지 적분을 해도 나머지 구간의 적분값은 0이 나오므로 $[a,b]$에서 적분한 것과 결과가 같습니다. 따라서 아래 등식이 성립합니다.
$$
\int_{a}^{b}xf(x)dx= \int_{-\infty}^{\infty}xf(x)dx
$$
확률밀도함수를 적분하여 평균이나 분산을구할 때, 구간을 $[-\infty, \infty]$ 로 설정해주면 됩니다.
<강의 영상>
https://www.youtube.com/watch?v=Py-oAEMMZlU
반응형
'기초과목 > 확률과통계 기초' 카테고리의 다른 글
| [확률과 통계 기초] 3-45. 정규분포의 발견 (2) 이항분포로 부터 (0) | 2025.11.22 |
|---|---|
| [확률과 통계 기초] 3-44. 정규분포의 발견 (1) 프롤로그 (0) | 2025.11.17 |
| [확률과 통계 기초] 3-43. 가능성이 변하는 연속확률변수의 확률함수 (0) | 2025.10.16 |
| [확률과 통계 기초] 3-42. 균등분포의 평균, 분산, 표준편차 (0) | 2025.10.07 |
| [확률과 통계 기초] 3-40. 구간 표현 익히기 [a,b] (a,b) (0) | 2025.08.30 |
| [확률과 통계 기초] 3-39. 연속확률분포의 분산과 표준편차 (0) | 2025.07.31 |
| [확률과 통계 기초] 3-38. 연속확률분포의 기댓값 (2) | 2025.07.30 |
| [확률과 통계 기초] 3-37. 균등분포 (2) | 2025.07.29 |
댓글